Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function mapping a nonempty compact convex set to itself there is a point such that . The simplest forms of Brouwer's theorem are for continuous functions from a closed interval in the real numbers to itself or from a closed disk to itself. A more general form than the latter is for continuous functions from a nonempty convex compact subset of Euclidean space to itself.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set is also called its size, when no confusion with other notions of size is possible.
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
In mathematics, Hausdorff dimension is a measure of roughness, or more specifically, fractal dimension, that was introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of dimensions for highly irregular or "rough" sets, this dimension is also commonly referred to as the Hausdorff–Besicovitch dimension.
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
In vector calculus and differential geometry the generalized Stokes theorem, also called the Stokes–Cartan theorem, is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. In particular, the fundamental theorem of calculus is the special case where the manifold is a line segment, Green’s theorem and Stokes' theorem are the cases of a surface in or and the divergence theorem is the case of a volume in Hence, the theorem is sometimes referred to as the Fundamental Theorem of Multivariate Calculus.
In mathematics, topology is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.
In mathematics, a curve is an object similar to a line, but that does not have to be straight.
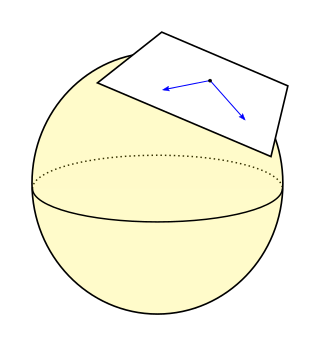
In differential geometry, a Riemannian manifold or Riemannian space(M, g), so called after the German mathematician Bernhard Riemann, is a real, smooth manifold M equipped with a positive-definite inner product gp on the tangent space TpM at each point p.
In topology, the Jordan curve theorem asserts that every Jordan curve divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points. Every continuous path connecting a point of one region to a point of the other intersects with the curve somewhere. While the theorem seems intuitively obvious, it takes some ingenuity to prove it by elementary means. "Although the JCT is one of the best known topological theorems, there are many, even among professional mathematicians, who have never read a proof of it.". More transparent proofs rely on the mathematical machinery of algebraic topology, and these lead to generalizations to higher-dimensional spaces.
In mathematical analysis, a space-filling curve is a curve whose range reaches every point in a higher dimensional region, typically the unit square. Because Giuseppe Peano (1858–1932) was the first to discover one, space-filling curves in the 2-dimensional plane are sometimes called Peano curves, but that phrase also refers to the Peano curve, the specific example of a space-filling curve found by Peano.
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In differential geometry, Mikhail Gromov's filling area conjecture asserts that the hemisphere has minimum area among the orientable surfaces that fill a closed curve of given length without introducing shortcuts between its points.
Eugen Otto Erwin Netto was a German mathematician. He was born in Halle and died in Giessen.
In mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies. For Jordan curves in the plane it is often referred to as the Jordan–Schoenflies theorem.
In mathematical analysis, an Osgood curve is a non-self-intersecting curve that has positive area. Despite its area, it is not possible for such a curve to cover any two-dimensional region, distinguishing them from space-filling curves. Osgood curves are named after William Fogg Osgood.
In topology, the Denjoy–Riesz theorem states that every compact set of totally disconnected points in the Euclidean plane can be covered by a continuous image of the unit interval, without self-intersections.
In geometry, smooth projective planes are special projective planes. The most prominent example of a smooth projective plane is the real projective plane . Its geometric operations of joining two distinct points by a line and of intersecting two lines in a point are not only continuous but even smooth. Similarly, the classical planes over the complex numbers, the quaternions, and the octonions are smooth planes. However, these are not the only such planes.
