Nilsemigroup

Last updated July 29, 2020

In mathematics, and more precisely in semigroup theory, a nilsemigroup or nilpotent semigroup is a semigroup whose every element is nilpotent.

Definitions

Formally, a semigroup S is a nilsemigroup if:

S contains 0 and
for each element a∈S, there exists a positive integer k such that a^k=0.

Finite nilsemigroups

Equivalent definitions exists for finite semigroup. A finite semigroup S is nilpotent if, equivalently:

$x_{1}\dots x_{n}=y_{1}\dots y_{n}$ for each $x_{i},y_{i}\in S$ , where $n$ is the cardinality of S.
The zero is the only idempotent of S.

Examples

The trivial semigroup of a single element is trivially a nilsemigroup.

The set of strictly upper triangular matrix, with matrix multiplication is nilpotent.

Let $I_{n}=[a,n]$ a bounded interval of positive real numbers. For x, y belonging to I, define $x\star _{n}y$ as $\min(x+y,n)$ . We now show that $\langle I,\star _{n}\rangle$ is a nilsemigroup whose zero is n. For each natural number k, kx is equal to $\min(kx,n)$ . For k at least equal to $\left\lceil {\frac {n-x}{x}}\right\rceil$ , kx equals n. This example generalize for any bounded interval of an Archimedean ordered semigroup.

Properties

A non-trivial nilsemigroup does not contain an identity element. It follows that the only nilpotent monoid is the trivial monoid.

The class of nilsemigroups is:

closed under taking subsemigroups
closed under taking quotients
closed under finite products
but is not closed under arbitrary direct product. Indeed, take the semigroup $S=\prod _{i\in \mathbb {N} }\langle I_{n},\star _{n}\rangle$ , where $\langle I_{n},\star _{n}\rangle$ is defined as above. The semigroup S is a direct product of nilsemigroups, however its contains no nilpotent element.

It follows that the class of nilsemigroups is not a variety of universal algebra. However, the set of finite nilsemigroups is a variety of finite semigroups. The variety of finite nilsemigroups is defined by the profinite equalities $x^{\omega }y=x^{\omega }=yx^{\omega }$ .

Related Research Articles

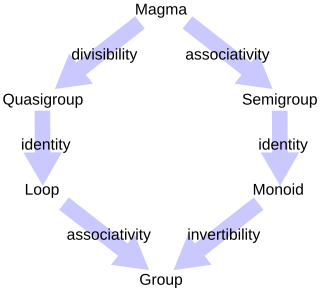
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element.

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation.

In mathematics, in particular abstract algebra, a graded ring is a ring such that the underlying additive group is a direct sum of abelian groups $such that . The index set is usually the set of nonnegative integers or the set of integers, but can be any monoid. The direct sum decomposition is usually referred to as gradation or grading .$

In linear algebra, a linear form is a linear map from a vector space to its field of scalars. In ℝⁿ, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the matrix product with the row vector on the left and the column vector on the right. In general, if V is a vector space over a field k, then a linear functional f is a function from V to k that is linear:

Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.

In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.

In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Roughly speaking, this means that if two functions $and in the RKHS are close in norm, i.e., is small, then and are also pointwise close, i.e., is small for all . The reverse does not need to be true.$

In linear algebra, the Gram matrix of a set of vectors $in an inner product space is the Hermitian matrix of inner products, whose entries are given by .$

In universal algebra, a variety of algebras or equational class is the class of all algebraic structures of a given signature satisfying a given set of identities. For example, the groups form a variety of algebras, as do the abelian groups, the rings, the monoids etc. According to Birkhoff's theorem, a class of algebraic structures of the same signature is a variety if and only if it is closed under the taking of homomorphic images, subalgebras and (direct) products. In the context of category theory, a variety of algebras, together with its homomorphisms, forms a category; these are usually called finitary algebraic categories.

In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.

In descriptive set theory, a tree on a set $is a collection of finite sequences of elements of such that every prefix of a sequence in the collection also belongs to the collection.$

In algebra, a presentation of a monoid is a description of a monoid in terms of a set $Σ$ of generators and a set of relations on the free monoid $Σ *$ generated by $Σ$ . The monoid is then presented as the quotient of the free monoid by these relations. This is an analogue of a group presentation in group theory.

In probability theory and statistical mechanics, the Gaussian free field (GFF) is a Gaussian random field, a central model of random surfaces. Sheffield (2007) gives a mathematical survey of the Gaussian free field.

In mathematics, a dissipative operator is a linear operator A defined on a linear subspace D(A) of Banach space X, taking values in X such that for all λ > 0 and all x ∈ D(A)

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is an abstract vector space possessing the structure of an inner product that allows length and angle to be measured. Furthermore, Hilbert spaces are complete: there are enough limits in the space to allow the techniques of calculus to be used.

In mathematics, more precisely in formal language theory, the profinite words are a generalization of the notion of finite words into a complete topological space. This notion allows the use of topology to study languages and finite semigroups. For example, profinite words are used to give an alternative characterization of the algebraic notion of a variety of finite semigroups.

In mathematics, and more precisely in semigroup theory, a variety of finite semigroups is a class of semigroups having some nice algebraic properties. Those classes can be defined in two distinct ways, using either algebraic notions or topological notions. Varieties of finite monoids, varieties of finite ordered semigroups and varieties of finite ordered monoids are defined similarly.

This article summarizes several identities in exterior calculus.

This is a glossary for the terminology in a mathematical field of functional analysis.

References

Pin, Jean-Éric (2018-06-15). Mathematical Foundations of Automata Theory (PDF). p. 198.
Grillet, P A (1995). Semigroups. CRC Press. p. 110. ISBN 978-0-8247-9662-4.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.