In physics, the no-cloning theorem states that it is impossible to create an identical copy of an arbitrary unknown quantum state. This no-go theorem of quantum mechanics was articulated by James Park in proving the impossibility of a simple perfect non-disturbing measurement scheme, in 1970 and rediscovered by Wootters and Zurek and by Dieks in 1982. It has profound implications in quantum computing and related fields. The state of one system can be entangled with the state of another system. For instance, one can use the controlled NOT gate and the Walsh–Hadamard gate to entangle two qubits. This is not cloning. No well-defined state can be attributed to a subsystem of an entangled state. Cloning is a process, the result of which is a separable state with identical factors.
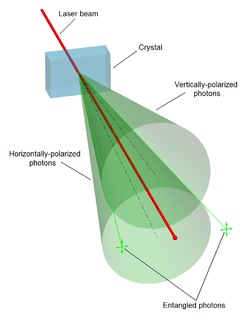
Quantum entanglement is the physical phenomenon that occurs when a pair or group of particles is generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the pair or group cannot be described independently of the state of the others, even when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics.
In quantum physics, a measurement is the testing or manipulation of a physical system in order to yield a numerical result. The predictions that quantum physics makes are in general probabilistic. The mathematical tools for making predictions about what measurement outcomes may occur were developed during the 20th century and make use of linear algebra and functional analysis.
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan. The quantum operation formalism describes not only unitary time evolution or symmetry transformations of isolated systems, but also the effects of measurement and transient interactions with an environment. In the context of quantum computation, a quantum operation is called a quantum channel.
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory. For a bipartite state , the conditional entropy is written , or , depending on the notation being used for the von Neumann entropy. The quantum conditional entropy was defined in terms of a conditional density operator by Nicolas Cerf and Chris Adami, who showed that quantum conditional entropies can be negative, something that is forbidden in classical physics. The negativity of quantum conditional entropy is a sufficient criterion for quantum non-separability.
Quantum metrology is the study of making high-resolution and highly sensitive measurements of physical parameters using quantum theory to describe the physical systems, particularly exploiting quantum entanglement and quantum squeezing. This field promises to develop measurement techniques that give better precision than the same measurement performed in a classical framework.
Quantum cloning is a process that takes an arbitrary, unknown quantum state and makes an exact copy without altering the original state in any way. Quantum cloning is forbidden by the laws of quantum mechanics as shown by the no cloning theorem, which states that there is no operation for cloning any arbitrary state perfectly. In Dirac notation, the process of quantum cloning is described by:
In quantum information theory, the channel-state duality refers to the correspondence between quantum channels and quantum states. Phrased differently, the duality is the isomorphism between completely positive maps (channels) from A to Cn×n, where A is a C*-algebra and Cn×n denotes the n×n complex entries, and positive linear functionals (states) on the tensor product
The topological entanglement entropy or topological entropy, usually denoted by γ, is a number characterizing many-body states that possess topological order.
In mathematics, in the area of quantum information geometry, the Bures metric or Helstrom metric defines an infinitesimal distance between density matrix operators defining quantum states. It is a quantum generalization of the Fisher information metric, and is identical to the Fubini–Study metric when restricted to the pure states alone.
Yambo is a computer software package for studying many-body theory aspects of solids and molecule systems. It calculates the excited state properties of physical systems from first principles, e.g., from quantum mechanics law without the use of empirical data. It is an open-source software released under the GNU General Public License (GPL). However the main development repository is provate and only a subset of the features available in the private repository are cloned into the public repository and thus distributed.
In quantum mechanics, especially in the study of open quantum systems, reduced dynamics refers to the time evolution of a density matrix for a system coupled to an environment. Consider a system and environment initially in the state and undergoing unitary evolution given by . Then the reduced dynamics of the system alone is simply
Decoy state quantum key distribution (QKD) protocol is the most widely implemented QKD scheme. Practical QKD systems use multi-photon sources, in contrast to the standard BB84 protocol, making them susceptible to photon number splitting (PNS) attacks. This would significantly limit the secure transmission rate or the maximum channel length in practical QKD systems. In decoy state technique, this fundamental weakness of practical QKD systems is addressed by using multiple intensity levels at the transmitter's source, i.e. qubits are transmitted by Alice using randomly chosen intensity levels, resulting in varying photon number statistics throughout the channel. At the end of the transmission Alice announces publicly which intensity level has been used for the transmission of each qubit. A successful PNS attack requires maintaining the bit error rate (BER) at the receiver's end, which can not be accomplished with multiple photon number statistics. By monitoring BERs associated with each intensity level, the two legitimate parties will be able to detect a PNS attack, with highly increased secure transmission rates or maximum channel lengths, making QKD systems suitable for practical applications.
Symmetry-protected topological (SPT) order is a kind of order in zero-temperature quantum-mechanical states of matter that have a symmetry and a finite energy gap.
Many quantum mechanical Hamiltonians are time dependent. How to solve problems where there is an explicit time dependence is an open subject nowadays. For problems of this kind it is of importance to look for constants of motion or invariants. For the harmonic oscillator it is possible to write several invariants, among them, the Ermakov–Lewis invariant which is developed below.
The min-entropy, in information theory, is the smallest of the Rényi family of entropies, corresponding to the most conservative way of measuring the unpredictability of a set of outcomes, as the negative logarithm of the probability of the most likely outcome. The various Rényi entropies are all equal for a uniform distribution, but measure the unpredictability of a nonuniform distribution in different ways. The min-entropy is never greater than the ordinary or Shannon entropy and that in turn is never greater than the Hartley or max-entropy, defined as the logarithm of the number of outcomes with nonzero probability.

Quantum thermodynamics is the study of the relations between two independent physical theories: thermodynamics and quantum mechanics. The two independent theories address the physical phenomena of light and matter. In 1905 Einstein argued that the requirement of consistency between thermodynamics and electromagnetism leads to the conclusion that light is quantized obtaining the relation . This paper is the dawn of quantum theory. In a few decades quantum theory became established with an independent set of rules. Currently quantum thermodynamics addresses the emergence of thermodynamic laws from quantum mechanics. It differs from quantum statistical mechanics in the emphasis on dynamical processes out of equilibrium. In addition there is a quest for the theory to be relevant for a single individual quantum system.
The no-hiding theorem proves that if information is lost from a system via decoherence, then it moves to the subspace of the environment and it cannot remain in the correlation between the system and the environment. This is a fundamental consequence of the linearity and unitarity of quantum mechanics. Thus, information is never lost. This has implications in black hole information paradox and in fact any process that tends to lose information completely. The no-hiding theorem is robust to imperfection in the physical process that seemingly destroys the original information.
In quantum information theory and quantum optics, the Gisin–Hughston–Jozsa–Wootters (GHJW) theorem is a result about the realization of a mixed state of a quantum system as an ensemble of pure quantum states and the relation between the corresponding purifications of the density operators. The theorem is named after physicists and mathematicians Nicolas Gisin, Lane P. Hughston, Richard Jozsa and William Wootters, though much of it was established decades earlier by Erwin Schrödinger. The result was also found independently by Nicolas Hadjisavvas building upon work by Ed Jaynes, while a significant part of it was likewise independently discovered by N. David Mermin. Thanks to its complicated history, it is also known as the HJW theorem and the Schrödinger–HJW theorem.
The quantum Cramér–Rao bound is the quantum analogue of the classical Cramér–Rao bound. It bounds the achievable precision in parameter estimation with a quantum system:






