In computational complexity theory, a branch of computer science, bounded-error probabilistic polynomial time (BPP) is the class of decision problems solvable by a probabilistic Turing machine in polynomial time with an error probability bounded by 1/3 for all instances. BPP is one of the largest practical classes of problems, meaning most problems of interest in BPP have efficient probabilistic algorithms that can be run quickly on real modern machines. BPP also contains P, the class of problems solvable in polynomial time with a deterministic machine, since a deterministic machine is a special case of a probabilistic machine.
The P versus NP problem is a major unsolved problem in theoretical computer science. Informally, it asks whether every problem whose solution can be quickly verified can also be quickly solved.

In computational complexity theory, NP is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.
In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem with input size n is in NC if there exist constants c and k such that it can be solved in time O((log n)c) using O(nk) parallel processors. Stephen Cook coined the name "Nick's class" after Nick Pippenger, who had done extensive research on circuits with polylogarithmic depth and polynomial size.
In computational complexity theory, a decision problem is P-complete if it is in P and every problem in P can be reduced to it by an appropriate reduction.
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient for a function to be called one-way.
A commitment scheme is a cryptographic primitive that allows one to commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later. Commitment schemes are designed so that a party cannot change the value or statement after they have committed to it: that is, commitment schemes are binding. Commitment schemes have important applications in a number of cryptographic protocols including secure coin flipping, zero-knowledge proofs, and secure computation.

In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.
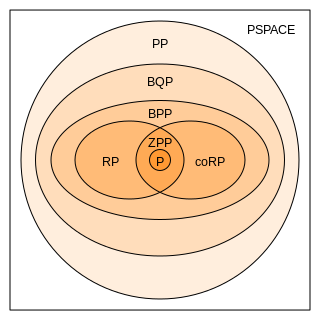
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time. The complexity class was defined by Gill in 1977.
In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem. For function problems, the output is not simply 'yes' or 'no'.
In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time .
In logic and theoretical computer science, and specifically proof theory and computational complexity theory, proof complexity is the field aiming to understand and analyse the computational resources that are required to prove or refute statements. Research in proof complexity is predominantly concerned with proving proof-length lower and upper bounds in various propositional proof systems. For example, among the major challenges of proof complexity is showing that the Frege system, the usual propositional calculus, does not admit polynomial-size proofs of all tautologies. Here the size of the proof is simply the number of symbols in it, and a proof is said to be of polynomial size if it is polynomial in the size of the tautology it proves.
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard E. Ladner, is a result asserting that, if P ≠ NP, then NPI is not empty; that is, NP contains problems that are neither in P nor NP-complete. Since it is also true that if NPI problems exist, then P ≠ NP, it follows that P = NP if and only if NPI is empty.
In computational complexity theory, the complexity class TFNP is the class of total function problems which can be solved in nondeterministic polynomial time. That is, it is the class of function problems that are guaranteed to have an answer, and this answer can be checked in polynomial time, or equivalently it is the subset of FNP where a solution is guaranteed to exist. The abbreviation TFNP stands for "Total Function Nondeterministic Polynomial".
In computational complexity theory, PostBQP is a complexity class consisting of all of the computational problems solvable in polynomial time on a quantum Turing machine with postselection and bounded error.
In computer science, PPAD is a complexity class introduced by Christos Papadimitriou in 1994. PPAD is a subclass of TFNP based on functions that can be shown to be total by a parity argument. The class attracted significant attention in the field of algorithmic game theory because it contains the problem of computing a Nash equilibrium: this problem was shown to be complete for PPAD by Daskalakis, Goldberg and Papadimitriou with at least 3 players and later extended by Chen and Deng to 2 players.
In computational complexity theory, the average-case complexity of an algorithm is the amount of some computational resource used by the algorithm, averaged over all possible inputs. It is frequently contrasted with worst-case complexity which considers the maximal complexity of the algorithm over all possible inputs.
In computational complexity theory, PPA is a complexity class, standing for "Polynomial Parity Argument". Introduced by Christos Papadimitriou in 1994, PPA is a subclass of TFNP. It is a class of search problems that can be shown to be total by an application of the handshaking lemma: any undirected graph that has a vertex whose degree is an odd number must have some other vertex whose degree is an odd number. This observation means that if we are given a graph and an odd-degree vertex, and we are asked to find some other odd-degree vertex, then we are searching for something that is guaranteed to exist.
In algorithmic game theory, a succinct game or a succinctly representable game is a game which may be represented in a size much smaller than its normal form representation. Without placing constraints on player utilities, describing a game of players, each facing strategies, requires listing utility values. Even trivial algorithms are capable of finding a Nash equilibrium in a time polynomial in the length of such a large input. A succinct game is of polynomial type if in a game represented by a string of length n the number of players, as well as the number of strategies of each player, is bounded by a polynomial in n.
In information theory, the computationally bounded adversary problem is a different way of looking at the problem of sending data over a noisy channel. In previous models the best that could be done was ensuring correct decoding for up to d/2 errors, where d was the Hamming distance of the code. The problem with doing it this way is that it does not take into consideration the actual amount of computing power available to the adversary. Rather, it only concerns itself with how many bits of a given code word can change and still have the message decode properly. In the computationally bounded adversary model the channel – the adversary – is restricted to only being able to perform a reasonable amount of computation to decide which bits of the code word need to change. In other words, this model does not need to consider how many errors can possibly be handled, but only how many errors could possibly be introduced given a reasonable amount of computing power on the part of the adversary. Once the channel has been given this restriction it becomes possible to construct codes that are both faster to encode and decode compared to previous methods that can also handle a large number of errors.




















