Partial permutation

Last updated November 07, 2024

In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.^[1]^[2]

Representation

It is common to consider the case when the set S is simply the set {1, 2, ..., n} of the first n integers. In this case, a partial permutation may be represented by a string of n symbols, some of which are distinct numbers in the range from 1 to $n$ and the remaining ones of which are a special "hole" symbol ◊. In this formulation, the domain U of the partial permutation consists of the positions in the string that do not contain a hole, and each such position is mapped to the number in that position. For instance, the string "1 ◊ 2" would represent the partial permutation that maps 1 to itself and maps 3 to 2.^[3] The seven partial permutations on two items are

◊◊, ◊1, ◊2, 1◊, 2◊, 12, 21.

Combinatorial enumeration

The number of partial permutations on n items, for n = 0, 1, 2, ..., is given by the integer sequence

1, 2, 7, 34, 209, 1546, 13327, 130922, 1441729, 17572114, 234662231, ... (sequence A002720 in the OEIS )

where the nth item in the sequence is given by the summation formula

\sum _{i=0}^{n}i!{\binom {n}{i}}^{2}

in which the ith term counts the number of partial permutations with support of size i, that is, the number of partial permutations with i non-hole entries. Alternatively, it can be computed by a recurrence relation

P(n)=2nP(n-1)-(n-1)^{2}P(n-2).

This is determined as follows:

$P(n-1)$ partial permutations where the final elements of each set are omitted:
$P(n-1)$ partial permutations where the final elements of each set map to each other.
$(n-1)P(n-1)$ partial permutations where the final element of the first set is included, but does not map to the final element of the second set
$(n-1)P(n-1)$ partial permutations where the final element of the second set is included, but does not map to the final element of the first set
$-(n-1)^{2}P(n-2)$ , the partial permutations included in both counts 3 and 4, those permutations where the final elements of both sets are included, but do not map to each other.

Restricted partial permutations

Some authors restrict partial permutations so that either the domain^[4] or the range^[3] of the bijection is forced to consist of the first k items in the set of n items being permuted, for some k. In the former case, a partial permutation of length k from an n-set is just a sequence of k terms from the n-set without repetition. (In elementary combinatorics, these objects are sometimes confusingly called "k-permutations" of the n-set.)

Related Research Articles

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

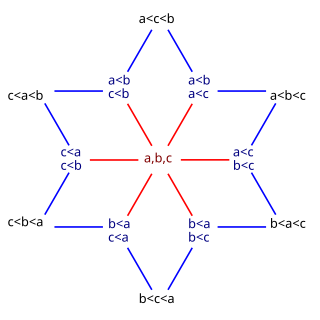
In mathematics, a permutation of a set can mean one of two different things:

In number theory and combinatorics, a partition of a non-negative integer $n$ , also called an integer partition, is a way of writing $n$ as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. For example, $4$ can be partitioned in five distinct ways:

In combinatorial mathematics, the theory of combinatorial species is an abstract, systematic method for deriving the generating functions of discrete structures, which allows one to not merely count these structures but give bijective proofs involving them. Examples of combinatorial species are graphs, permutations, trees, and so on; each of these has an associated generating function which counts how many structures there are of a certain size. One goal of species theory is to be able to analyse complicated structures by describing them in terms of transformations and combinations of simpler structures. These operations correspond to equivalent manipulations of generating functions, so producing such functions for complicated structures is much easier than with other methods. The theory was introduced, carefully elaborated and applied by Canadian researchers around André Joyal.

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, the term combinatorial proof is often used to mean either of two types of mathematical proof:

In mathematics, particularly in combinatorics, given a family of sets, here called a collection C, a transversal (also called a cross-section) is a set containing exactly one element from each member of the collection. When the sets of the collection are mutually disjoint, each element of the transversal corresponds to exactly one member of C (the set it is a member of). If the original sets are not disjoint, there are two possibilities for the definition of a transversal:

In combinatorics, bijective proof is a proof technique for proving that two sets have equally many elements, or that the sets in two combinatorial classes have equal size, by finding a bijective function that maps one set one-to-one onto the other. This technique can be useful as a way of finding a formula for the number of elements of certain sets, by corresponding them with other sets that are easier to count. Additionally, the nature of the bijection itself often provides powerful insights into each or both of the sets.

In mathematics, and in particular in combinatorics, the combinatorial number system of degree k, also referred to as combinadics, or the Macaulay representation of an integer, is a correspondence between natural numbers N and k-combinations. The combinations are represented as strictly decreasing sequences c_k > ... > c₂ > c₁ ≥ 0 where each c_i corresponds to the index of a chosen element in a given k-combination. Distinct numbers correspond to distinct k-combinations, and produce them in lexicographic order. The numbers less than $correspond to all k -combinations of {0, 1, ..., n - 1}. The correspondence does not depend on the size n of the set that the k -combinations are taken from, so it can be interpreted as a map from N to the k -combinations taken from N; in this view the correspondence is a bijection.$

<span class="mw-page-title-main">Ordered Bell number</span> Number of weak orderings

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of $elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.$

In mathematics, especially order theory, the interval order for a collection of intervals on the real line is the partial order corresponding to their left-to-right precedence relation—one interval, I₁, being considered less than another, I₂, if I₁ is completely to the left of I₂. More formally, a countable poset $is an interval order if and only if there exists a bijection from to a set of real intervals, so, such that for any we have in exactly when .$

In computer science and the study of combinatorics on words, a partial word is a string that may contain a number of "do not know" or "do not care" symbols i.e. placeholders in the string where the symbol value is not known or not specified. More formally, a partial word is a partial function $where is some finite alphabet. If u (k) is not defined for some then the unknown element at place k in the string is called a "hole". In regular expressions (following the POSIX standard) a hole is represented by the metacharacter ".". For example, aab.ab.b is a partial word of length 8 over the alphabet A ={a, b} in which the fourth and seventh characters are holes.$

In combinatorial mathematics and theoretical computer science, a (classical) permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of entries representing the result of applying the permutation to the sequence 123...; for instance the sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the entries of π has the same relative order as all of the entries of σ.

In mathematics and in particular in combinatorics, the Lehmer code is a particular way to encode each possible permutation of a sequence of n numbers. It is an instance of a scheme for numbering permutations and is an example of an inversion table.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the plane trees with a given set of leaves, the ways of inserting parentheses into a sequence, and the ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin

In mathematics and computer science, a stack-sortable permutation is a permutation whose elements may be sorted by an algorithm whose internal storage is limited to a single stack data structure. The stack-sortable permutations are exactly the permutations that do not contain the permutation pattern 231; they are counted by the Catalan numbers, and may be placed in bijection with many other combinatorial objects with the same counting function including Dyck paths and binary trees.

In the mathematical study of combinatorics on words, a parameter word is a string over a given alphabet having some number of wildcard characters. The set of strings matching a given parameter word is called a parameter set or combinatorial cube. Parameter words can be composed, to produce smaller subcubes of a given combinatorial cube. They have applications in Ramsey theory and in computer science in the detection of duplicate code.

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

References

↑ Straubing, Howard (1983), "A combinatorial proof of the Cayley-Hamilton theorem", Discrete Mathematics, 43 (2–3): 273–279, doi: 10.1016/0012-365X(83)90164-4 , MR 0685635 .
↑ Ku, C. Y.; Leader, I. (2006), "An Erdős-Ko-Rado theorem for partial permutations", Discrete Mathematics , 306 (1): 74–86, doi: 10.1016/j.disc.2005.11.007 , MR 2202076 .
1 2 Claesson, Anders; Jelínek, Vít; Jelínková, Eva; Kitaev, Sergey (2011), "Pattern avoidance in partial permutations", Electronic Journal of Combinatorics, 18 (1): Paper 25, 41, arXiv: 1005.2216 , doi:10.37236/512, MR 2770130 .
↑ Burstein, Alexander; Lankham, Isaiah (2010), "Restricted patience sorting and barred pattern avoidance", Permutation patterns, London Math. Soc. Lecture Note Ser., vol. 376, Cambridge: Cambridge Univ. Press, pp. 233–257, arXiv: math/0512122 , doi:10.1017/CBO9780511902499.013, ISBN 978-0-521-72834-8, MR 2732833 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Straubing, Howard (1983), "A combinatorial proof of the Cayley-Hamilton theorem", Discrete Mathematics, 43 (2–3): 273–279, doi: 10.1016/0012-365X(83)90164-4 , MR 0685635 .

[2] Ku, C. Y.; Leader, I. (2006), "An Erdős-Ko-Rado theorem for partial permutations", Discrete Mathematics , 306 (1): 74–86, doi: 10.1016/j.disc.2005.11.007 , MR 2202076 .

[cjjk-3] 1 2 Claesson, Anders; Jelínek, Vít; Jelínková, Eva; Kitaev, Sergey (2011), "Pattern avoidance in partial permutations", Electronic Journal of Combinatorics, 18 (1): Paper 25, 41, arXiv: 1005.2216 , doi:10.37236/512, MR 2770130 .

[4] Burstein, Alexander; Lankham, Isaiah (2010), "Restricted patience sorting and barred pattern avoidance", Permutation patterns, London Math. Soc. Lecture Note Ser., vol. 376, Cambridge: Cambridge Univ. Press, pp. 233–257, arXiv: math/0512122 , doi:10.1017/CBO9780511902499.013, ISBN 978-0-521-72834-8, MR 2732833 .

[1]

[2]

[3]

[4]