Partial word

Last updated

In computer science and the study of combinatorics on words, a partial word is a string that may contain a number of "do not know" or "do not care" symbols i.e. placeholders in the string where the symbol value is not known or not specified. More formally, a partial word is a partial function where is some finite alphabet. If u(k) is not defined for some then the unknown element at place k in the string is called a "hole". In regular expressions (following the POSIX standard) a hole is represented by the metacharacter ".". For example, aab.ab.b is a partial word of length 8 over the alphabet A ={a,b} in which the fourth and seventh characters are holes. [1]

Contents

Algorithms

Several algorithms have been developed for the problem of "string matching with don't cares", in which the input is a long text and a shorter partial word and the goal is to find all strings in the text that match the given partial word. [2] [3] [4]

Applications

A compatibility graph of partial words Cube-face-intersection-graph.svg
A compatibility graph of partial words

Two partial words are said to be compatible when they have the same length and when every position that is a non-wildcard in both of them has the same character in both. If one forms an undirected graph with a vertex for each partial word in a collection of partial words, and an edge for each compatible pair, then the cliques of this graph come from sets of partial words that all match at least one common string. This graph-theoretical interpretation of compatibility of partial words plays a key role in the proof of hardness of approximation of the clique problem, in which a collection of partial words representing successful runs of a probabilistically checkable proof verifier has a large clique if and only if there exists a valid proof of an underlying NP-complete problem. [5]

The faces (subcubes) of an -dimensional hypercube can be described by partial words of length over a binary alphabet, whose symbols are the Cartesian coordinates of the hypercube vertices (e.g., 0 or 1 for a unit cube). The dimension of a subcube, in this representation, equals the number of don't-care symbols it contains. The same representation may also be used to describe the implicants of Boolean functions. [6]

Partial words may be generalized to parametric words, in which some of the "do not know" symbols are marked as being equal to each other. A partial word is a special case of a parametric word in which each do not know symbol may be substituted by a character independently of all of the other ones. [7]

Related Research Articles

Bipartite graph graph of two disjoint sets in which every vertex in one set is connected to at least one in the other

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

Clique problem computational problem of finding cliques in a graph

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

In computational linguistics and computer science, edit distance is a way of quantifying how dissimilar two strings are to one another by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T.

In theoretical computer science, the subgraph isomorphism problem is a computational task in which two graphs G and H are given as input, and one must determine whether G contains a subgraph that is isomorphic to H. Subgraph isomorphism is a generalization of both the maximum clique problem and the problem of testing whether a graph contains a Hamiltonian cycle, and is therefore NP-complete. However certain other cases of subgraph isomorphism may be solved in polynomial time.

Independent set (graph theory) set of vertices in a graph, no two of which are adjacent

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set of vertices such that for every two vertices in , there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . The size of an independent set is the number of vertices it contains. Independent sets have also been called internally stable sets.

Perfect graph type of graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if for all we have .

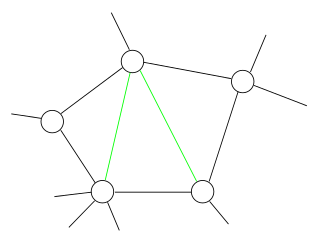
Chordal graph

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.

Boxicity

In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.

In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In the mathematical fields of graph theory and combinatorial optimization, the bipartite dimension or biclique cover number of a graph G = (V, E) is the minimum number of bicliques, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).

Combinatorics on words is a fairly new field of mathematics, branching from combinatorics, which focuses on the study of words and formal languages. The subject looks at letters or symbols, and the sequences they form. Combinatorics on words affects various areas of mathematical study, including algebra and computer science. There have been a wide range of contributions to the field. Some of the first work was on square-free words by Axel Thue in the early 1900s. He and colleagues observed patterns within words and tried to explain them. As time went on, combinatorics on words became useful in the study of algorithms and coding. It led to developments in abstract algebra and answering open questions.

In graph theory, the graph bandwidth problem is to label the n vertices vi of a graph G with distinct integers f(vi) so that the quantity is minimized . The problem may be visualized as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement.

In graph theory, a partial cube is a graph that is isometric to a subgraph of a hypercube. In other words, a partial cube can be identified with a subgraph of a hypercube in such a way that the distance between any two vertices in the partial cube is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.

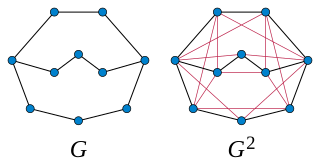
Graph power

In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.

Matroid parity problem

In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.

In the mathematical study of combinatorics on words, a parametric word is a string over a given alphabet having some number of wildcard characters. The set of strings matching a given parametric word is called a combinatorial cube. Parametric words can be composed, to produce smaller subcubes of a given combinatorial cube. They have applications in Ramsey theory and in computer science in the detection of duplicate code.

Algorithmic Combinatorics on Partial Words is a book in the area of combinatorics on words, and more specifically on partial words. It was written by Francine Blanchet-Sadri, and published in 2008 by Chapman & Hall/CRC in their Discrete Mathematics and its Applications book series.

References

  1. ↑ Blanchet-Sadri, Francine (2008), Algorithmic Combinatorics on Partial Words, Discrete Mathematics and its Applications, Boca Raton, Florida: Chapman & Hall/CRC, ISBN   978-1-4200-6092-8, MR   2384993
  2. ↑ Pinter, Ron Y. (1985), "Efficient string matching with don't-care patterns", Combinatorial algorithms on words (Maratea, 1984), NATO Adv. Sci. Inst. Ser. F Comput. Systems Sci., 12, Springer, Berlin, pp. 11–29, MR   0815329
  3. ↑ Manber, Udi; Baeza-Yates, Ricardo (1991), "An algorithm for string matching with a sequence of don't cares", Information Processing Letters , 37 (3): 133–136, doi:10.1016/0020-0190(91)90032-D, MR   1095695
  4. ↑ Kalai, Adam (2002), "Efficient pattern-matching with don't cares", in Eppstein, David (ed.), Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms, January 6-8, 2002, San Francisco, CA, USA, ACM and SIAM, pp. 655–656
  5. ↑ Feige, U.; Goldwasser, S.; Lovász, L.; Safra, S; Szegedy, M. (1991), "Approximating clique is almost NP-complete", Proc. 32nd IEEE Symp. on Foundations of Computer Science, pp. 2–12, doi:10.1109/SFCS.1991.185341, ISBN   0-8186-2445-0
  6. ↑ Karnaugh, Maurice (1953), "The map method for synthesis of combinational logic circuits", Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics, 1953: 593–599, doi:10.1109/TCE.1953.6371932, MR   0069032
  7. ↑ Prömel, Hans Jürgen (2002), "Large numbers, Knuth's arrow notation, and Ramsey theory", Synthese , 133 (1–2): 87–105, doi:10.1023/A:1020879709125, JSTOR   20117296, MR   1950045
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.