In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. Numerical analysis naturally finds application in all fields of engineering and the physical sciences, but in the 21st century also the life sciences, social sciences, medicine, business and even the arts have adopted elements of scientific computations. The growth in computing power has revolutionized the use of realistic mathematical models in science and engineering, and subtle numerical analysis is required to implement these detailed models of the world. For example, ordinary differential equations appear in celestial mechanics ; numerical linear algebra is important for data analysis; stochastic differential equations and Markov chains are essential in simulating living cells for medicine and biology.
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context. One is numerical linear algebra and the other is algorithms for solving ordinary and partial differential equations by discrete approximation.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, furniture, attire, soil strata, prostheses and biological tissue. Structural analysis employs the fields of applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures.

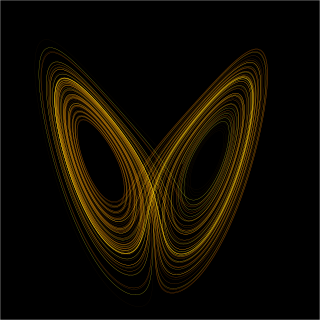
A differential equation is a mathematical equation that relates some function with its derivatives. In applications, the functions usually represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Because such relations are extremely common, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
In numerical analysis, a superconvergent or supraconvergent method is one which converges faster than generally expected. For example, in the Finite Element Method approximation to Poisson's equation in two dimensions, using piecewise linear elements, the average error in the gradient is first order. However under certain conditions it's possible to recover the gradient at certain locations within each element to second order.
Numerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations. including fluid mechanics, acoustics, electromagnetics, fracture mechanics, and contact mechanics.
In numerical analysis, the Lax equivalence theorem is the fundamental theorem in the analysis of finite difference methods for the numerical solution of partial differential equations. It states that for a consistent finite difference method for a well-posed linear initial value problem, the method is convergent if and only if it is stable.
In the numerical solution of partial differential equations, a topic in mathematics, the spectral element method (SEM) is a formulation of the finite element method (FEM) that uses high degree piecewise polynomials as basis functions. The spectral element method was introduced in a 1984 paper by A. T. Patera.
In mathematics, in particular numerical analysis, the FETI method is an iterative substructuring method for solving systems of linear equations from the finite element method for the solution of elliptic partial differential equations, in particular in computational mechanics In each iteration, FETI requires the solution of a Neumann problem in each substructure and the solution of a coarse problem. The simplest version of FETI with no preconditioner in the substructure is scalable with the number of substructures but the condition number grows polynomially with the number of elements per substructure. FETI with a preconditioner consisting of the solution of a Dirichlet problem in each substructure is scalable with the number of substructures and its condition number grows only polylogarithmically with the number of elements per substructure. The coarse space in FETI consists of the nullspace on each substructure.
hp-FEM is a general version of the finite element method (FEM), a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size (h) and polynomial degree (p). The origins of hp-FEM date back to the pioneering work of Ivo Babuška et al. who discovered that the finite element method converges exponentially fast when the mesh is refined using a suitable combination of h-refinements (dividing elements into smaller ones) and p-refinements. The exponential convergence makes the method a very attractive choice compared to most other finite element methods which only converge with an algebraic rate. The exponential convergence of the hp-FEM was not only predicted theoretically but also observed by numerous independent researchers.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.

The homotopy analysis method (HAM) is a semi-analytical technique to solve nonlinear ordinary/partial differential equations. The homotopy analysis method employs the concept of the homotopy from topology to generate a convergent series solution for nonlinear systems. This is enabled by utilizing a homotopy-Maclaurin series to deal with the nonlinearities in the system.
In numerical analysis, order of accuracy quantifies the rate of convergence of a numerical approximation of a differential equation to the exact solution. Consider , the exact solution to a differential equation in an appropriate normed space . Consider a numerical approximation , where is a parameter characterizing the approximation, such as the step size in a finite difference scheme or the diameter of the cells in a finite element method. The numerical solution is said to be th-order accurate if the error, is proportional to the step-size to the th power;

In numerical mathematics, the gradient discretisation method (GDM) is a framework which contains classical and recent numerical schemes for diffusion problems of various kinds: linear or non-linear, steady-state or time-dependent. The schemes may be conforming or non-conforming, and may rely on very general polygonal or polyhedral meshes.








