
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. An example of a 3×3 Latin square is
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.

In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
In the mathematical study of permutations and permutation patterns, a superpattern or universal permutation is a permutation that contains all of the patterns of a given length. More specifically, a k-superpattern contains all possible patterns of length k.
The Stanley–Wilf conjecture, formulated independently by Richard P. Stanley and Herbert Wilf in the late 1980s, states that the growth rate of every proper permutation class is singly exponential. It was proved by Adam Marcus and Gábor Tardos (2004) and is no longer a conjecture. Marcus and Tardos actually proved a different conjecture, due to Zoltán Füredi and Péter Hajnal (1992), which had been shown to imply the Stanley–Wilf conjecture by Klazar (2000).
In the mathematical subject of group theory, the Hanna Neumann conjecture is a statement about the rank of the intersection of two finitely generated subgroups of a free group. The conjecture was posed by Hanna Neumann in 1957. In 2011, a strengthened version of the conjecture was proved independently by Joel Friedman and by Igor Mineyev.

Gábor Tardos is a Hungarian mathematician, currently a professor at Central European University and previously a Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science. He is the younger brother of Éva Tardos.

In combinatorial mathematics, a separable permutation is a permutation that can be obtained from the trivial permutation 1 by direct sums and skew sums. Separable permutations may be characterized by the forbidden permutation patterns 2413 and 3142; they are also the permutations whose permutation graphs are cographs and the permutations that realize the series-parallel partial orders. It is possible to test in polynomial time whether a given separable permutation is a pattern in a larger permutation, or to find the longest common subpattern of two separable permutations.
In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of digits representing the result of applying the permutation to the digit sequence 123...; for instance the digit sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the digits of π has the same relative order as all of the digits of σ.
In the study of permutation patterns, there has been considerable interest in enumerating specific permutation classes, especially those with relatively few basis elements. This area of study has turned up unexpected instances of Wilf equivalence, where two seemingly-unrelated permutation classes have the same numbers of permutations of each length.
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.
In discrete geometry, the Erdős distinct distances problem states that every set of points in the plane has a nearly-linear number of distinct distances. It was posed by Paul Erdős in 1946 and almost proven by Larry Guth and Nets Katz in 2015.
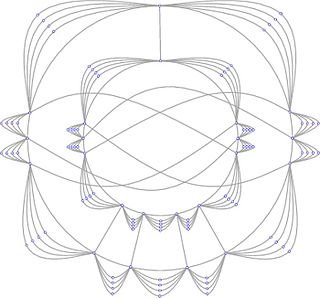
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.
Richard Alejandro Arratia is a mathematician noted for his work in combinatorics and probability theory.
Adam Wade Marcus is an American mathematician. He holds the Chair of Combinatorial Analysis in the Institute of Mathematics at the École Polytechnique Fédérale de Lausanne. The team of Marcus, Daniel Spielman and Nikhil Srivastava was awarded the Pólya Prize in 2014 for their resolution of the Kadison–Singer problem and later the Michael and Sheila Held Prize in 2021 for their solution to long-standing conjectures in the study of Ramanujan graphs.
In the study of permutations and permutation patterns, Wilf equivalence is an equivalence relation on permutation classes. Two permutation classes are Wilf equivalent when they have the same numbers of permutations of each possible length, or equivalently if they have the same generating functions. The equivalence classes for Wilf equivalence are called Wilf classes; they are the combinatorial classes of permutation classes. The counting functions and Wilf equivalences among many specific permutation classes are known.
In the mathematics of permutations, a layered permutation is a permutation that reverses contiguous blocks of elements. Equivalently, it is the direct sum of decreasing permutations.












