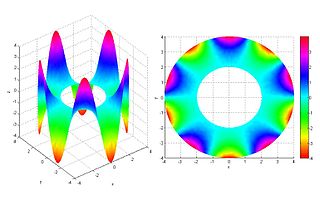
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R where U is an open subset of Rn that satisfies Laplace's equation, i.e.

In physics and mathematics, the heat equation is a partial differential equation that describes how the distribution of some quantity evolves over time in a solid medium, as it spontaneously flows from places where it is higher towards places where it is lower. It is a special case of the diffusion equation.
Calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations that commonly occur in science. The spherical harmonics are a complete set of orthogonal functions on the sphere, and thus may be used to represent functions defined on the surface of a sphere, just as circular functions are used to represent functions on a circle via Fourier series. Like the sines and cosines in Fourier series, the spherical harmonics may be organized by (spatial) angular frequency, as seen in the rows of functions in the illustration on the right. Further, spherical harmonics are basis functions for SO(3), the group of rotations in three dimensions, and thus play a central role in the group theoretic discussion of SO(3).
In mathematics, a Green's function of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions is its impulse response.
In mathematics, integral equations are equations in which an unknown function appears under an integral sign.
In mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory. In its general nature, it is a singular integral operator, defined by convolution with a function having a mathematical singularity at the origin, the Newtonian kernel Γ which is the fundamental solution of the Laplace equation. It is named for Isaac Newton, who first discovered it and proved that it was a harmonic function in the special case of three variables, where it served as the fundamental gravitational potential in Newton's law of universal gravitation. In modern potential theory, the Newtonian potential is instead thought of as an electrostatic potential.
In quantum field theory, a quartic interaction is a type of self-interaction in a scalar field. Other types of quartic interactions may be found under the topic of four-fermion interactions. A classical free scalar field satisfies the Klein–Gordon equation. If a scalar field is denoted , a quartic interaction is represented by adding a potential term to the Lagrangian density. The coupling constant is dimensionless in 4-dimensional spacetime.
In mathematics, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorems and is a result in Fredholm theory. It may be expressed in several ways, as a theorem of linear algebra, a theorem of integral equations, or as a theorem on Fredholm operators. Part of the result states that a non-zero complex number in the spectrum of a compact operator is an eigenvalue.

In mathematics, an elliptic boundary value problem is a special kind of boundary value problem which can be thought of as the stable state of an evolution problem. For example, the Dirichlet problem for the Laplacian gives the eventual distribution of heat in a room several hours after the heating is turned on.
In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates. There are two kinds: the regular solid harmonics , which vanish at the origin and the irregular solid harmonics , which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately:
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.
The obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problems. The problem is to find the equilibrium position of an elastic membrane whose boundary is held fixed, and which is constrained to lie above a given obstacle. It is deeply related to the study of minimal surfaces and the capacity of a set in potential theory as well. Applications include the study of fluid filtration in porous media, constrained heating, elasto-plasticity, optimal control, and financial mathematics.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
In mathematics, the Schauder estimates are a collection of results due to Juliusz Schauder concerning the regularity of solutions to linear, uniformly elliptic partial differential equations. The estimates say that when the equation has appropriately smooth terms and appropriately smooth solutions, then the Hölder norm of the solution can be controlled in terms of the Hölder norms for the coefficient and source terms. Since these estimates assume by hypothesis the existence of a solution, they are called a priori estimates.
In mathematics, the method of steepest descent or stationary-phase method or saddle-point method is an extension of Laplace's method for approximating an integral, where one deforms a contour integral in the complex plane to pass near a stationary point, in roughly the direction of steepest descent or stationary phase. The saddle-point approximation is used with integrals in the complex plane, whereas Laplace’s method is used with real integrals.
In mathematics, the Neumann–Poincaré operator or Poincaré–Neumann operator, named after Carl Neumann and Henri Poincaré, is a non-self-adjoint compact operator introduced by Poincaré to solve boundary value problems for the Laplacian on bounded domains in Euclidean space. Within the language of potential theory it reduces the partial differential equation to an integral equation on the boundary to which the theory of Fredholm operators can be applied. The theory is particularly simple in two dimensions—the case treated in detail in this article—where it is related to complex function theory, the conjugate Beurling transform or complex Hilbert transform and the Fredholm eigenvalues of bounded planar domains.