
The Alcubierre drive is a speculative warp drive idea according to which a spacecraft could achieve apparent faster-than-light travel by contracting space in front of it and expanding space behind it, under the assumption that a configurable energy-density field lower than that of vacuum could be created. Proposed by theoretical physicist Miguel Alcubierre in 1994, the Alcubierre drive is based on a solution of Einstein's field equations. Since those solutions are metric tensors, the Alcubierre drive is also referred to as Alcubierre metric.

Loop quantum gravity (LQG) is a theory of quantum gravity, which aims to reconcile quantum mechanics and general relativity, incorporating matter of the Standard Model into the framework established for the intrinsic quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Einstein's geometric formulation rather than the treatment of gravity as a mysterious mechanism (force). As a theory, LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale above the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.
In particle physics, the hypothetical dilaton particle is a particle of a scalar field that appears in theories with extra dimensions when the volume of the compactified dimensions varies. It appears as a radion in Kaluza–Klein theory's compactifications of extra dimensions. In Brans–Dicke theory of gravity, Newton's constant is not presumed to be constant but instead 1/G is replaced by a scalar field and the associated particle is the dilaton.
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation similar to general relativity. The theory was first proposed by Élie Cartan in 1922. Einstein–Cartan theory is the simplest Poincaré gauge theory.

In physics, the topological structure of spinfoam or spin foam consists of two-dimensional faces representing a configuration required by functional integration to obtain a Feynman's path integral description of quantum gravity. These structures are employed in loop quantum gravity as a version of quantum foam.
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity (LQG), a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units. As a result, its value is currently fixed by matching the semiclassical black hole entropy, as calculated by Stephen Hawking, and the counting of microstates in loop quantum gravity.
In the ADM formulation of general relativity, spacetime is split into spatial slices and a time axis. The basic variables are taken to be the induced metric on the spatial slice and the metric's conjugate momentum , which is related to the extrinsic curvature and is a measure of how the induced metric evolves in time. These are the metric canonical coordinates.

The Wheeler–DeWitt equation for theoretical physics and applied mathematics, is a field equation attributed to John Archibald Wheeler and Bryce DeWitt. The equation attempts to mathematically combine the ideas of quantum mechanics and general relativity, a step towards a theory of quantum gravity.
The BF model or BF theory is a topological field, which when quantized, becomes a topological quantum field theory. BF stands for background field B and F, as can be seen below, are also the variables appearing in the Lagrangian of the theory, which is helpful as a mnemonic device.
The Barrett–Crane model is a model in quantum gravity, first published in 1998, which was defined using the Plebanski action.
In acoustics and fluid dynamics, an acoustic metric is a metric that describes the signal-carrying properties of a given particulate medium.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.

In general relativity, post-Newtonian expansions are used for finding an approximate solution of Einstein field equations for the metric tensor. The approximations are expanded in small parameters that express orders of deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields sometimes it is preferable to solve the complete equations numerically. This method is a common mark of effective field theories. In the limit, when the small parameters are equal to 0, the post-Newtonian expansion reduces to Newton's law of gravity.
f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.
In mathematical physics, de Sitter invariant special relativity is the speculative idea that the fundamental symmetry group of spacetime is the indefinite orthogonal group SO(4,1), that of de Sitter space. In the standard theory of general relativity, de Sitter space is a highly symmetrical special vacuum solution, which requires a cosmological constant or the stress–energy of a constant scalar field to sustain.
In the field of theoretical physics, the Holst action is an equivalent formulation of the Palatini action for General Relativity (GR) in terms of vierbeins by adding a part of a topological term (Nieh-Yan) which does not alter the classical equations of motion as long as there is no torsion,
In general relativity, the Hamilton–Jacobi–Einstein equation (HJEE) or Einstein–Hamilton–Jacobi equation (EHJE) is an equation in the Hamiltonian formulation of geometrodynamics in superspace, cast in the "geometrodynamics era" around the 1960s, by Asher Peres in 1962 and others. It is an attempt to reformulate general relativity in such a way that it resembles quantum theory within a semiclassical approximation, much like the correspondence between quantum mechanics and classical mechanics.
In the ADM formulation of general relativity one splits spacetime into spatial slices and time, the basic variables are taken to be the induced metric, , on the spatial slice, and its conjugate momentum variable related to the extrinsic curvature, ,. These are the metric canonical coordinates.
The Einstein–Hilbert action for general relativity was first formulated purely in terms of the space-time metric. To take the metric and affine connection as independent variables in the action principle was first considered by Palatini. It is called a first order formulation as the variables to vary over involve only up to first derivatives in the action and so doesn't overcomplicate the Euler–Lagrange equations with higher derivative terms. The tetradic Palatini action is another first-order formulation of the Einstein–Hilbert action in terms of a different pair of independent variables, known as frame fields and the spin connection. The use of frame fields and spin connections are essential in the formulation of a generally covariant fermionic action which couples fermions to gravity when added to the tetradic Palatini action.
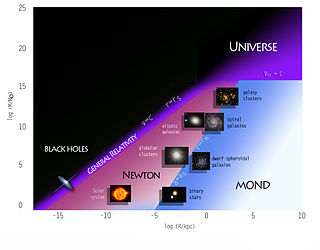
Extended theories of gravity are alternative theories of gravity developed from the exact starting points investigated first by Albert Einstein and Hilbert. These are theories describing gravity, which are metric theory, "a linear connection" or related affine theories, or metric-affine gravitation theory. Rather than trying to discover correct calculations for the matter side of the Einstein field equations; which include inflation, dark energy, dark matter, large-scale structure, and possibly quantum gravity; it is proposed, instead, to change the gravitational side of the equation.














