A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

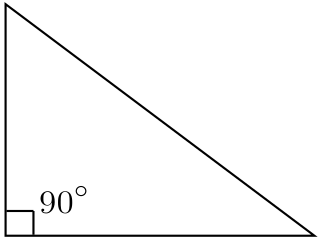
A right triangle or right-angled triangle is a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry.
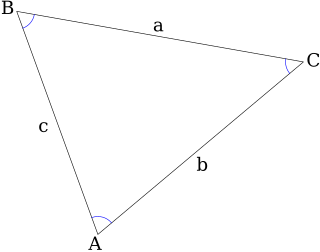
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. According to the law,

In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three.

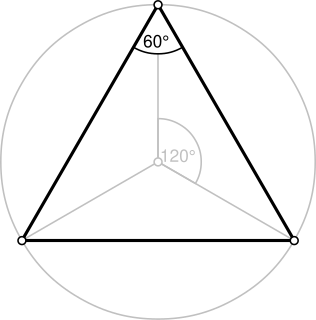
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, who is said to have offered an ox, probably to the god Apollo, as a sacrifice of thanksgiving for the discovery, but it is sometimes attributed to Pythagoras.

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.
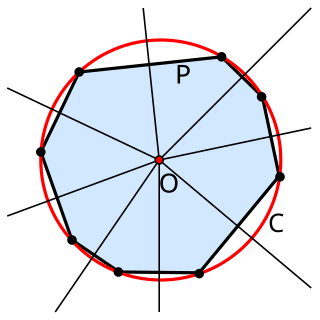
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
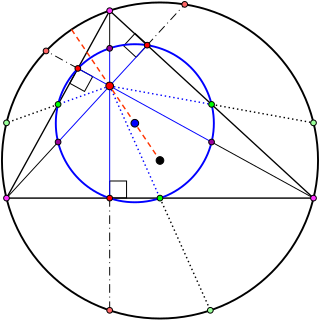
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.

In geometry, a set of Johnson circles comprises three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more intersection point. If any two of the circles happen to osculate, they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure. The concept is named after Roger Arthur Johnson.
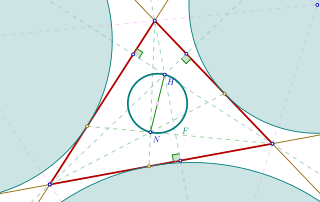
In geometry, the Fuhrmann circle of a triangle, named after the German Wilhelm Fuhrmann (1833–1904), is the circle with a diameter of the line segment between the orthocenter and the Nagel point . This circle is identical with the circumcircle of the Fuhrmann triangle.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states
An acute triangle is a triangle with three acute angles. An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle.
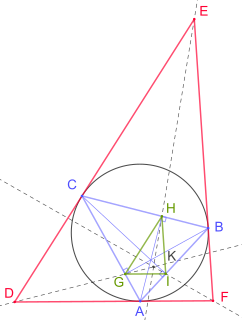
In geometry, the tangential triangle of a reference triangle is the triangle whose sides are on the tangent lines to the reference triangle's circumcircle at the reference triangle's vertices. Thus the incircle of the tangential triangle coincides with the circumcircle of the reference triangle.






















