
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering.

In mathematics, a complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a symbol called the imaginary unit, and satisfying the equation i2 = −1. Because no "real" number satisfies this equation, i was called an imaginary number by René Descartes. For the complex number a + bi, a is called the real part and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

In mathematics, an exponential function is a function of the form
In mathematics, the Laplace transform, named after its inventor Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms linear differential equations into algebraic equations and convolution into multiplication.

In electrical engineering, electrical impedance is the measure of the opposition that a circuit presents to a current when a voltage is applied.

In mathematics, the complex plane or z-plane is the plane associated with complex coordinate system, formed or established by the real axis and the perpendicular imaginary axis. It can be thought of as a modified Cartesian plane, with the real part of a complex number represented by a displacement along the x-axis, and the imaginary part by a displacement along the y-axis.
A resistor–capacitor circuit, or RC filter or RC network, is an electric circuit composed of resistors and capacitors. It may be driven by a voltage or current source and these will produce different responses. A first order RC circuit is composed of one resistor and one capacitor and is the simplest type of RC circuit.
In signal processing, specifically control theory, bounded-input, bounded-output (BIBO) stability is a form of stability for linear signals and systems that take inputs. If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.
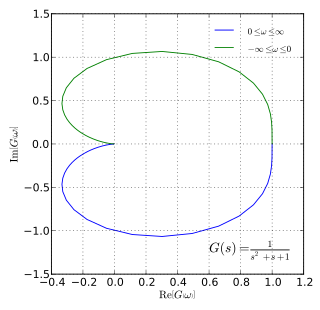
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer Felix Strecker at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a dynamical system. Because it only looks at the Nyquist plot of the open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system. As a result, it can be applied to systems defined by non-rational functions, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with multiple inputs and multiple outputs, such as control systems for airplanes.
Foster's reactance theorem is an important theorem in the fields of electrical network analysis and synthesis. The theorem states that the reactance of a passive, lossless two-terminal (one-port) network always strictly monotonically increases with frequency. It is easily seen that the reactances of inductors and capacitors individually increase with frequency and from that basis a proof for passive lossless networks generally can be constructed. The proof of the theorem was presented by Ronald Martin Foster in 1924, although the principle had been published earlier by Foster's colleagues at American Telephone & Telegraph.
In mathematics, the super-logarithm is one of the two inverse functions of tetration. Just as exponentiation has two inverse functions, roots and logarithms, tetration has two inverse functions, super-roots and super-logarithms. There are several ways of interpreting super-logarithms:
Network synthesis filters are signal processing filters designed by the network synthesis method. The method has produced several important classes of filter including the Butterworth filter, the Chebyshev filter and the Elliptic filter. It was originally intended to be applied to the design of passive linear analogue filters but its results can also be applied to implementations in active filters and digital filters. The essence of the method is to obtain the component values of the filter from a given rational function representing the desired transfer function.
An equivalent impedance is an equivalent circuit of an electrical network of impedance elements which presents the same impedance between all pairs of terminals as did the given network. This article describes mathematical transformations between some passive, linear impedance networks commonly found in electronic circuits.

Wilhelm Cauer was a German mathematician and scientist. He is most noted for his work on the analysis and synthesis of electrical filters and his work marked the beginning of the field of network synthesis. Prior to his work, electronic filter design used techniques which accurately predicted filter behaviour only under unrealistic conditions. This required a certain amount of experience on the part of the designer to choose suitable sections to include in the design. Cauer placed the field on a firm mathematical footing, providing tools that could produce exact solutions to a given specification for the design of an electronic filter.
Otto Walter Heinrich Oscar Brune undertook some key investigations into network synthesis at the Massachusetts Institute of Technology (MIT) where he graduated in 1929. His doctoral thesis was supervised by Wilhelm Cauer and Ernst Guillemin, who the latter ascribed to Brune the laying of "the mathematical foundation for modern realization theory".
Analogue filters are a basic building block of signal processing much used in electronics. Amongst their many applications are the separation of an audio signal before application to bass, mid-range, and tweeter loudspeakers; the combining and later separation of multiple telephone conversations onto a single channel; the selection of a chosen radio station in a radio receiver and rejection of others.
In mathematics, a function defined on a region of the complex plane is said to be of bounded type if it is equal to the ratio of two analytic functions bounded in that region. But more generally, a function is of bounded type in a region if and only if is analytic on and has a harmonic majorant on where . Being the ratio of two bounded analytic functions is a sufficient condition for a function to be of bounded type, and if is simply connected the condition is also necessary.

In electrical circuit theory, a port is a pair of terminals connecting an electrical network or circuit to an external circuit, as a point of entry or exit for electrical energy. A port consists of two nodes (terminals) connected to an outside circuit which meets the port condition - the currents flowing into the two nodes must be equal and opposite.
Network synthesis is a design technique for linear electrical circuits. Synthesis starts from a prescribed impedance function of frequency or frequency response and then determines the possible networks that will produce the required response. The technique is to be compared to network analysis in which the response of a given circuit is calculated. Prior to network synthesis, only network analysis was available, but this requires that one already knows what form of circuit is to be analysed. There is no guarantee that the chosen circuit will be the closest possible match to the desired response, nor that the circuit is the simplest possible. Network synthesis directly addresses both these issues. Network synthesis has historically been concerned with synthesising passive networks, but is not limited to such circuits.
Richards' theorem is a mathematical result due to Paul I. Richards in 1947. The theorem states that for,










