Probabilistic logic network

Last updated

A probabilistic logic network (PLN) is a conceptual, mathematical and computational approach to uncertain inference. It was inspired by logic programming and it uses probabilities in place of crisp (true/false) truth values, and fractional uncertainty in place of crisp known/unknown values. In order to carry out effective reasoning in real-world circumstances, artificial intelligence software handles uncertainty. Previous approaches to uncertain inference do not have the breadth of scope required to provide an integrated treatment of the disparate forms of cognitively critical uncertainty as they manifest themselves within the various forms of pragmatic inference. Going beyond prior probabilistic approaches to uncertain inference, PLN encompasses uncertain logic with such ideas as induction, abduction, analogy, fuzziness and speculation, and reasoning about time and causality. [1]

Contents

PLN was developed by Ben Goertzel, Matt Ikle, Izabela Lyon Freire Goertzel, and Ari Heljakka for use as a cognitive algorithm used by MindAgents within the OpenCog Core. PLN was developed originally for use within the Novamente Cognition Engine. [2]

Goal

The basic goal of a PLN is to provide accurate probabilistic inference in a way that is compatible with both term logic and predicate logic and scales up to operate in real-time on large dynamic knowledge bases. [2]

The goal underlying the theoretical development of PLN has been the creation of practical software systems carrying out complex inferences based on uncertain knowledge and drawing uncertain conclusions. PLN has been designed to allow basic probabilistic inference to interact with other kinds of inference such as intensional inference, fuzzy inference, and higher-order inference using quantifiers, variables, and combinators, and be a more convenient approach than Bayesian networks (or other conventional approaches) for the purpose of interfacing basic probabilistic inference with these other sorts of inference. In addition, the inference rules are formulated in such a way as to avoid the paradoxes of Dempster–Shafer theory.

Implementation

PLN begins with a term logic foundation and then adds on elements of probabilistic and combinatory logic, as well as some aspects of predicate logic and autoepistemic logic, to form a complete inference system, tailored for easy integration with software components embodying other (not explicitly logical) aspects of intelligence.

PLN represents truth values as intervals, but with different semantics than in imprecise probability theory. In addition to the interpretation of truth in a probabilistic fashion, a truth value in PLN also has an associated amount of certainty. This generalizes the notion of truth values used in autoepistemic logic, where truth values are either known or unknown and when known, are either true or false.

The current version of PLN has been used in narrow-AI applications such as the inference of biological hypotheses from knowledge extracted from biological texts via language processing, and to assist the reinforcement learning of an embodied agent, in a simple virtual world, as it is taught to play "fetch".

Related Research Articles

Knowledge representation and reasoning is a field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can use to solve complex tasks, such as diagnosing a medical condition or having a natural-language dialog. Knowledge representation incorporates findings from psychology about how humans solve problems and represent knowledge, in order to design formalisms that make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning.

In linguistics and philosophy, a vague predicate is one which gives rise to borderline cases. For example, the English adjective "tall" is vague since it is not clearly true or false for someone of middling height. By contrast, the word "prime" is not vague since every number is definitively either prime or not. Vagueness is commonly diagnosed by a predicate's ability to give rise to the Sorites paradox. Vagueness is separate from ambiguity, in which an expression has multiple denotations. For instance the word "bank" is ambiguous since it can refer either to a river bank or to a financial institution, but there are no borderline cases between both interpretations.

Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.

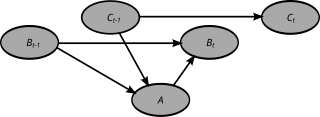
<span class="mw-page-title-main">Dynamic Bayesian network</span> Probabilistic graphical model

A dynamic Bayesian network (DBN) is a Bayesian network (BN) which relates variables to each other over adjacent time steps.

The expression computational intelligence (CI) usually refers to the ability of a computer to learn a specific task from data or experimental observation. Even though it is commonly considered a synonym of soft computing, there is still no commonly accepted definition of computational intelligence.

The autoepistemic logic is a formal logic for the representation and reasoning of knowledge about knowledge. While propositional logic can only express facts, autoepistemic logic can express knowledge and lack of knowledge about facts.

A Markov logic network (MLN) is a probabilistic logic which applies the ideas of a Markov network to first-order logic, defining probability distributions on possible worlds on any given domain.

Probabilistic logic involves the use of probability and logic to deal with uncertain situations. Probabilistic logic extends traditional logic truth tables with probabilistic expressions. A difficulty of probabilistic logics is their tendency to multiply the computational complexities of their probabilistic and logical components. Other difficulties include the possibility of counter-intuitive results, such as in case of belief fusion in Dempster–Shafer theory. Source trust and epistemic uncertainty about the probabilities they provide, such as defined in subjective logic, are additional elements to consider. The need to deal with a broad variety of contexts and issues has led to many different proposals.

Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics and to a lesser extent computer science. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.

<span class="mw-page-title-main">Ben Goertzel</span> American computer scientist and AI researcher

Ben Goertzel is a computer scientist, artificial intelligence researcher, and businessman. He helped popularize the term 'artificial general intelligence'.

A semantic reasoner, reasoning engine, rules engine, or simply a reasoner, is a piece of software able to infer logical consequences from a set of asserted facts or axioms. The notion of a semantic reasoner generalizes that of an inference engine, by providing a richer set of mechanisms to work with. The inference rules are commonly specified by means of an ontology language, and often a description logic language. Many reasoners use first-order predicate logic to perform reasoning; inference commonly proceeds by forward chaining and backward chaining. There are also examples of probabilistic reasoners, including non-axiomatic reasoning systems, and probabilistic logic networks.

Type-2 fuzzy sets and systems generalize standard Type-1 fuzzy sets and systems so that more uncertainty can be handled. From the beginning of fuzzy sets, criticism was made about the fact that the membership function of a type-1 fuzzy set has no uncertainty associated with it, something that seems to contradict the word fuzzy, since that word has the connotation of much uncertainty. So, what does one do when there is uncertainty about the value of the membership function? The answer to this question was provided in 1975 by the inventor of fuzzy sets, Lotfi A. Zadeh, when he proposed more sophisticated kinds of fuzzy sets, the first of which he called a "type-2 fuzzy set". A type-2 fuzzy set lets us incorporate uncertainty about the membership function into fuzzy set theory, and is a way to address the above criticism of type-1 fuzzy sets head-on. And, if there is no uncertainty, then a type-2 fuzzy set reduces to a type-1 fuzzy set, which is analogous to probability reducing to determinism when unpredictability vanishes.

<span class="mw-page-title-main">OpenCog</span> Project for an open source artificial intelligence framework

OpenCog is a project that aims to build an open source artificial intelligence framework. OpenCog Prime is an architecture for robot and virtual embodied cognition that defines a set of interacting components designed to give rise to human-equivalent artificial general intelligence (AGI) as an emergent phenomenon of the whole system. OpenCog Prime's design is primarily the work of Ben Goertzel while the OpenCog framework is intended as a generic framework for broad-based AGI research. Research utilizing OpenCog has been published in journals and presented at conferences and workshops including the annual Conference on Artificial General Intelligence. OpenCog is released under the terms of the GNU Affero General Public License.

NetWeaver Developer is a knowledgebase development system. This article

  1. gives a brief history of the system,
  2. summarizes key features of the software,
  3. is a bit of a primer, describing basic attributes of a NetWeaver knowledgebase, and
  4. provides secondary references that independently document some of the NetWeaver applications developed since the late 1980s.

Uncertain inference was first described by C. J. van Rijsbergen as a way to formally define a query and document relationship in Information retrieval. This formalization is a logical implication with an attached measure of uncertainty.

In information technology a reasoning system is a software system that generates conclusions from available knowledge using logical techniques such as deduction and induction. Reasoning systems play an important role in the implementation of artificial intelligence and knowledge-based systems.

<span class="mw-page-title-main">Probabilistic soft logic</span>

Probabilistic Soft Logic (PSL) is a statistical relational learning (SRL) framework for modeling probabilistic and relational domains. It is applicable to a variety of machine learning problems, such as collective classification, entity resolution, link prediction, and ontology alignment. PSL combines two tools: first-order logic, with its ability to succinctly represent complex phenomena, and probabilistic graphical models, which capture the uncertainty and incompleteness inherent in real-world knowledge. More specifically, PSL uses "soft" logic as its logical component and Markov random fields as its statistical model. PSL provides sophisticated inference techniques for finding the most likely answer (i.e. the maximum a posteriori (MAP) state). The "softening" of the logical formulas makes inference a polynomial time operation rather than an NP-hard operation.

Knowledge crystals are web-based information objects that are used in scientific information production. Especially, they are used in open assessments designed to support societal decisions. They act as current best answers to specific research questions. They are produced and distributed openly using crowdsourcing and scientific criticism.

This glossary of artificial intelligence is a list of definitions of terms and concepts relevant to the study of artificial intelligence (AI), its subdisciplines, and related fields. Related glossaries include Glossary of computer science, Glossary of robotics, and Glossary of machine vision.

In logic, an infinite-valued logic is a many-valued logic in which truth values comprise a continuous range. Traditionally, in Aristotle's logic, logic other than bivalent logic was abnormal, as the law of the excluded middle precluded more than two possible values for any proposition. Modern three-valued logic allows for an additional possible truth value and is an example of finite-valued logic in which truth values are discrete, rather than continuous. Infinite-valued logic comprises continuous fuzzy logic, though fuzzy logic in some of its forms can further encompass finite-valued logic. For example, finite-valued logic can be applied in Boolean-valued modeling, description logics, and defuzzification of fuzzy logic.

References

See also

References

  1. ↑ "Probabilistic logic networks - OpenCog". wiki.opencog.org. Retrieved 2024-05-27.
  2. 1 2 Goertzel, Ben; Iklé, Matthew; Freire Goertzel, Izabella; Heljakka, Ari (November 11, 2008). Probabilistic Logic Networks (2nd ed.). ISBN   9780387768717.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.