Protein fragment library

Last updated May 03, 2019

Protein backbone fragment libraries have been used successfully in a variety of structural biology applications, including homology modeling,^[1] de novo structure prediction,^[2]^[3]^[4] and structure determination.^[5] By reducing the complexity of the search space, these fragment libraries enable more rapid search of conformational space, leading to more efficient and accurate models.

Structural biology study of molecular structures in biology

Structural biology is a branch of molecular biology, biochemistry, and biophysics concerned with the molecular structure of biological macromolecules, how they acquire the structures they have, and how alterations in their structures affect their function. This subject is of great interest to biologists because macromolecules carry out most of the functions of cells, and it is only by coiling into specific three-dimensional shapes that they are able to perform these functions. This architecture, the "tertiary structure" of molecules, depends in a complicated way on each molecule's basic composition, or "primary structure."

Homology modeling, also known as comparative modeling of protein, refers to constructing an atomic-resolution model of the "target" protein from its amino acid sequence and an experimental three-dimensional structure of a related homologous protein. Homology modeling relies on the identification of one or more known protein structures likely to resemble the structure of the query sequence, and on the production of an alignment that maps residues in the query sequence to residues in the template sequence. It has been shown that protein structures are more conserved than protein sequences amongst homologues, but sequences falling below a 20% sequence identity can have very different structure.

In computational biology, de novo protein structure prediction refers to an algorithmic process by which protein tertiary structure is predicted from its amino acid primary sequence. The problem itself has occupied leading scientists for decades while still remaining unsolved. According to Science, the problem remains one of the top 125 outstanding issues in modern science. At present, some of the most successful methods have a reasonable probability of predicting the folds of small, single-domain proteins within 1.5 angstroms over the entire structure.

Motivation

Proteins can adopt an exponential number of states when modeled discretely. Typically, a protein's conformations are represented as sets of dihedral angles, bond lengths, and bond angles between all connected atoms. The most common simplification is to assume ideal bond lengths and bond angles. However, this still leaves the phi-psi angles of the backbone, and up to four dihedral angles for each side chain, leading to a worst case complexity of k^6*n possible states of the protein, where n is the number of residues and k is the number of discrete states modeled for each dihedral angle. In order to reduce the conformational space, one can use protein fragment libraries rather than explicitly model every phi-psi angle.

Protein biological molecule consisting of chains of amino acid residues

Proteins are large biomolecules, or macromolecules, consisting of one or more long chains of amino acid residues. Proteins perform a vast array of functions within organisms, including catalysing metabolic reactions, DNA replication, responding to stimuli, providing structure to cells and organisms, and transporting molecules from one location to another. Proteins differ from one another primarily in their sequence of amino acids, which is dictated by the nucleotide sequence of their genes, and which usually results in protein folding into a specific three-dimensional structure that determines its activity.

A dihedral angle is the angle between two intersecting planes. In chemistry it is the angle between planes through two sets of three atoms, having two atoms in common. In solid geometry it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimension, a dihedral angle represents the angle between two hyperplanes.

In molecular geometry, bond length or bond distance is the average distance between nuclei of two bonded atoms in a molecule. It is a transferable property of a bond between atoms of fixed types, relatively independent of the rest of the molecule.

Fragments are short segments of the peptide backbone, typically from 5 to 15 residues long, and do not include the side chains. They may specify the location of just the C-alpha atoms if it is a reduced atom representation, or all the backbone heavy atoms (N, C-alpha, C carbonyl, O). Note that side chains are typically not modeled using the fragment library approach. To model discrete states of a side chain, one could use a rotamer library approach.^[6]

Amino acid Organic compounds containing amine and carboxylic groups

Amino acids are organic compounds containing amine (-NH₂) and carboxyl (-COOH) functional groups, along with a side chain (R group) specific to each amino acid. The key elements of an amino acid are carbon (C), hydrogen (H), oxygen (O), and nitrogen (N), although other elements are found in the side chains of certain amino acids. About 500 naturally occurring amino acids are known (though only 20 appear in the genetic code) and can be classified in many ways. They can be classified according to the core structural functional groups' locations as alpha- (α-), beta- (β-), gamma- (γ-) or delta- (δ-) amino acids; other categories relate to polarity, pH level, and side chain group type (aliphatic, acyclic, aromatic, containing hydroxyl or sulfur, etc.). In the form of proteins, amino acid residues form the second-largest component (water is the largest) of human muscles and other tissues. Beyond their role as residues in proteins, amino acids participate in a number of processes such as neurotransmitter transport and biosynthesis.

This approach operates under the assumption that local interactions play a large role in stabilizing the overall protein conformation. In any short sequence, the molecular forces constrain the structure, leading to only a small number of possible conformations, which can be modeled by fragments. Indeed, according to Levinthal's paradox, a protein could not possibly sample all possible conformations within a biologically reasonable amount of time. Locally stabilized structures would reduce the search space and allow proteins to fold on the order of milliseconds.

Levinthal's paradox is a thought experiment, also constituting a self-reference in the theory of protein folding. In 1969, Cyrus Levinthal noted that, because of the very large number of degrees of freedom in an unfolded polypeptide chain, the molecule has an astronomical number of possible conformations. An estimate of 3³⁰⁰ or 10¹⁴³ was made in one of his papers (often incorrectly cited as the 1968 paper). For example, a polypeptide of 100 residues will have 99 peptide bonds, and therefore 198 different phi and psi bond angles. If each of these bond angles can be in one of three stable conformations, the protein may misfold into a maximum of 3¹⁹⁸ different conformations (including any possible folding redundancy). Therefore, if a protein were to attain its correctly folded configuration by sequentially sampling all the possible conformations, it would require a time longer than the age of the universe to arrive at its correct native conformation. This is true even if conformations are sampled at rapid (nanosecond or picosecond) rates. The "paradox" is that most small proteins fold spontaneously on a millisecond or even microsecond time scale. The solution to this paradox has been established by computational approaches to protein structure prediction.

Construction

Clustering of similar fragments. Centroid is shown in blue. ProteinFragmentClustering.png — Clustering of similar fragments. Centroid is shown in blue.

Libraries of these fragments are constructed from an analysis of the Protein Data Bank (PDB). First, a representative subset of the PDB is chosen which should cover a diverse array of structures, preferably at a good resolution. Then, for each structure, every set of n consecutive residues is taken as a sample fragment. The samples are then clustered into k groups, based upon how similar they are to each other in spatial configuration, using algorithms such as k-means clustering. The parameters n and k are chosen according to the application (see discussion on complexity below). The centroids of the clusters are then taken to represent the fragment. Further optimization can be performed to ensure that the centroid possesses ideal bond geometry, as it was derived by averaging other geometries. ^[7]

The Protein Data Bank (PDB) is a database for the three-dimensional structural data of large biological molecules, such as proteins and nucleic acids. The data, typically obtained by X-ray crystallography, NMR spectroscopy, or, increasingly, cryo-electron microscopy, and submitted by biologists and biochemists from around the world, are freely accessible on the Internet via the websites of its member organisations. The PDB is overseen by an organization called the Worldwide Protein Data Bank, wwPDB.

k-means clustering is a method of vector quantization, originally from signal processing, that is popular for cluster analysis in data mining. k-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster. This results in a partitioning of the data space into Voronoi cells.

Centroid mean ("average") position of all the points in the shape; mean position of all the points in all of the coordinate directions; point at which a cutout of the shape could be perfectly balanced on the tip of a pin

In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.

Because the fragments are derived from structures that exist in nature, the segment of backbone they represent will have realistic bonding geometries. This helps avoid having to explore the full space of conformation angles, much of which would lead to unrealistic geometries.

The clustering above can be performed without regard to the identities of the residues, or it can be residue-specific.^[2] That is, for any given input sequence of amino acids, a clustering can be derived using only samples found in the PDB with the same sequence in the k-mer fragment. This requires more computational work than deriving a sequence-independent fragment library but can potentially produce more accurate models. Conversely, a larger sample set is required, and one may not achieve full coverage.

Example use: loop modeling

Loop of length 10 constructed using 6 fragments, each of length 4. Only overlaps of 2 were used in this 2D model. Anchor points are circled. LoopConstructionUsingFragments.png — Loop of length 10 constructed using 6 fragments, each of length 4. Only overlaps of 2 were used in this 2D model. Anchor points are circled.

In homology modeling, a common application of fragment libraries is to model the loops of the structure. Typically, the alpha helices and beta sheets are threaded against a template structure, but the loops in between are not specified and need to be predicted. Finding the loop with the optimal configuration is NP-hard. To reduce the conformational space that needs to be explored, one can model the loop as a series of overlapping fragments. The space can then be sampled, or if the space is now small enough, exhaustively enumerated.

One approach for exhaustive enumeration goes as follows.^[1] Loop construction begins by aligning all possible fragments to overlap with the three residues at the N terminus of the loop (the anchor point). Then all possible choices for a second fragment are aligned to (all possible choices of) the first fragment, ensuring that the last three residues of the first fragment overlap with the first three residues of the second fragment. This ensures that the fragment chain forms realistic angles both within the fragment and between fragments. This is then repeated until a loop with the correct length of residues is constructed.

The loop must both begin at the anchor on the N side and end at the anchor on the C side. Each loop must therefore be tested to see if its last few residues overlap with the C terminal anchor. Very few of these exponential numbers of candidate loops will close the loop. After filtering out loops that don't close, one must then determine which loop has the optimal configuration, as determined by having the lowest energy using some molecular mechanics force field.

Complexity

The complexity of the state space is still exponential in the number of residues, even after using fragment libraries. However, the degree of the exponent is reduced. For a library of F-mer fragments, with L fragments in the library, and to model a chain of N residues overlapping each fragment by 3, there will be L^[N/(F-3)]+1 possible chains. ^[7] This is much less than the K^N possibilities if explicitly modeling the phi-psi angles as K possible combinations, as the complexity grows at a degree smaller than N.

The complexity increases in L, the size of the fragment library. However, libraries with more fragments will capture a greater diversity of fragment structures, so there is a trade off in the accuracy of the model vs the speed of exploring the search space. This choice governs what K is used when performing the clustering.

Additionally, for any fixed L, the diversity of structures capable of being modeled decreases as the length of the fragments increases. Shorter fragments are more capable of covering the diverse array of structures found in the PDB than longer ones. Recently, it was shown that libraries of up to length 15 are capable of modeling 91% of the fragments in the PDB to within 2.0 angstroms. ^[8]

Related Research Articles

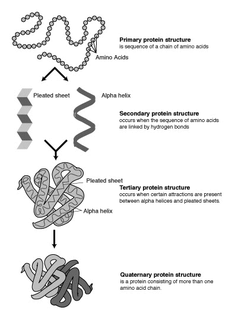
The alpha helix (α-helix) is a common motif in the secondary structure of proteins and is a right hand-helix conformation in which every backbone N−H group donates a hydrogen bond to the backbone C=O group of the amino acid located three or four residues earlier along the protein sequence.

The β-sheet is a common motif of regular secondary structure in proteins. Beta sheets consist of beta strands connected laterally by at least two or three backbone hydrogen bonds, forming a generally twisted, pleated sheet. A β-strand is a stretch of polypeptide chain typically 3 to 10 amino acids long with backbone in an extended conformation. The supramolecular association of β-sheets has been implicated in formation of the protein aggregates and fibrils observed in many human diseases, notably the amyloidoses such as Alzheimer's disease.

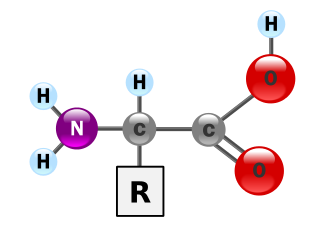
Protein secondary structure is the three dimensional form of local segments of proteins. The two most common secondary structural elements are alpha helices and beta sheets, though beta turns and omega loops occur as well. Secondary structure elements typically spontaneously form as an intermediate before the protein folds into its three dimensional tertiary structure.

Protein structure prediction is the inference of the three-dimensional structure of a protein from its amino acid sequence—that is, the prediction of its folding and its secondary and tertiary structure from its primary structure. Structure prediction is fundamentally different from the inverse problem of protein design. Protein structure prediction is one of the most important goals pursued by bioinformatics and theoretical chemistry; it is highly important in medicine and biotechnology. Every two years, the performance of current methods is assessed in the CASP experiment. A continuous evaluation of protein structure prediction web servers is performed by the community project CAMEO3D.

Structural alignment attempts to establish homology between two or more polymer structures based on their shape and three-dimensional conformation. This process is usually applied to protein tertiary structures but can also be used for large RNA molecules. In contrast to simple structural superposition, where at least some equivalent residues of the two structures are known, structural alignment requires no a priori knowledge of equivalent positions. Structural alignment is a valuable tool for the comparison of proteins with low sequence similarity, where evolutionary relationships between proteins cannot be easily detected by standard sequence alignment techniques. Structural alignment can therefore be used to imply evolutionary relationships between proteins that share very little common sequence. However, caution should be used in using the results as evidence for shared evolutionary ancestry because of the possible confounding effects of convergent evolution by which multiple unrelated amino acid sequences converge on a common tertiary structure.

A Ramachandran plot, originally developed in 1963 by G. N. Ramachandran, C. Ramakrishnan, and V. Sasisekharan, is a way to visualize energetically allowed regions for backbone dihedral angles ψ against φ of amino acid residues in protein structure. The figure at left illustrates the definition of the φ and ψ backbone dihedral angles. The ω angle at the peptide bond is normally 180°, since the partial-double-bond character keeps the peptide planar. The figure at top right shows the allowed φ,ψ backbone conformational regions from the Ramachandran et al. 1963 and 1968 hard-sphere calculations: full radius in solid outline, reduced radius in dashed, and relaxed tau (N-Cα-C) angle in dotted lines. Because dihedral angle values are circular and 0° is the same as 360°, the edges of the Ramachandran plot "wrap" right-to-left and bottom-to-top. For instance, the small strip of allowed values along the lower-left edge of the plot are a continuation of the large, extended-chain region at upper left.

Nuclear magnetic resonance spectroscopy of proteins is a field of structural biology in which NMR spectroscopy is used to obtain information about the structure and dynamics of proteins, and also nucleic acids, and their complexes. The field was pioneered by Richard R. Ernst and Kurt Wüthrich at the ETH, and by Ad Bax, Marius Clore, and Angela Gronenborn at the NIH, among others. Structure determination by NMR spectroscopy usually consists of several phases, each using a separate set of highly specialized techniques. The sample is prepared, measurements are made, interpretive approaches are applied, and a structure is calculated and validated.

ICM stands for Internal Coordinate Mechanics and was first designed and built to predict low-energy conformations of molecules by sampling the space of internal coordinates defining molecular geometry. In ICM each molecule is constructed as a tree from an entry atom where each next atom is built iteratively from the preceding three atoms via three internal variables. The rings kept rigid or imposed via additional restraints.

A turn is an element of secondary structure in proteins where the polypeptide chain reverses its overall direction.

A polyproline helix is a type of protein secondary structure which occurs in proteins comprising repeating proline residues. A left-handed polyproline II helix is formed when sequential residues all adopt (φ,ψ) backbone dihedral angles of roughly and have trans isomers of their peptide bonds. This PPII conformation is also common in proteins and polypeptides with other amino acids apart from proline. Similarly, a more compact right-handed polyproline I helix is formed when sequential residues all adopt (φ,ψ) backbone dihedral angles of roughly and have cis isomers of their peptide bonds. Of the twenty common naturally occurring amino acids, only proline is likely to adopt the cis isomer of the peptide bond, specifically the X-Pro peptide bond; steric and electronic factors heavily favor the trans isomer in most other peptide bonds. However, peptide bonds that replace proline with another N-substituted amino acid are also likely to adopt the cis isomer.

Conformational entropy is the entropy associated with the number of conformations of a molecule. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but also be used for polysaccharides and other molecules. To calculate the conformational entropy, the possible conformations of the molecule may first be discretized into a finite number of states, usually characterized by unique combinations of certain structural parameters, each of which has been assigned an energy. In proteins, backbone dihedral angles and side chain rotamers are commonly used as parameters, and in RNA the base pairing pattern may be used. These characteristics are used to define the degrees of freedom. The conformational entropy associated with a particular structure or state, such as an alpha-helix, a folded or an unfolded protein structure, is then dependent on the probability of the occupancy of that structure.

Loop modeling is a problem in protein structure prediction requiring the prediction of the conformations of loop regions in proteins with or without the use of a structural template. Computer programs that solve these problems have been used to research a broad range of scientific topics from ADP to breast cancer. Because protein function is determined by its shape and the physiochemical properties of its exposed surface, it is important to create an accurate model for protein/ligand interaction studies. The problem arises often in homology modeling, where the tertiary structure of an amino acid sequence is predicted based on a sequence alignment to a template, or a second sequence whose structure is known. Because loops have highly variable sequences even within a given structural motif or protein fold, they often correspond to unaligned regions in sequence alignments; they also tend to be located at the solvent-exposed surface of globular proteins and thus are more conformationally flexible. Consequently, they often cannot be modeled using standard homology modeling techniques. More constrained versions of loop modeling are also used in the data fitting stages of solving a protein structure by X-ray crystallography, because loops can correspond to regions of low electron density and are therefore difficult to resolve.

FoldX is a protein design algorithm that uses an empirical force field. It can determine the energetic effect of point mutations as well as the interaction energy of protein complexes. FoldX can mutate protein and DNA side chains using a probability-based rotamer library, while exploring alternative conformations of the surrounding side chains.

I-sites are short sequence-structure motifs that are mined from the Protein Data Bank (PDB) that correlate strongly with three-dimensional structural elements. These sequence-structure motifs are used for the local structure prediction of proteins. Local structure can be expressed as fragments or as backbone angles. Locations in the protein sequence that have high confidence I-sites predictions may be the initiation sites of folding. I-sites have also been identified as discrete models for folding pathways. I-sites consist of about 250 motifs. Each motif has an amino acid profile, a fragment structure and optionally, a 4-dimensional tensor of pairwise sequence covariance.

Graphical models have become powerful frameworks for protein structure prediction, protein–protein interaction, and free energy calculations for protein structures. Using a graphical model to represent the protein structure allows the solution of many problems including secondary structure prediction, protein-protein interactions, protein-drug interaction, and free energy calculations.

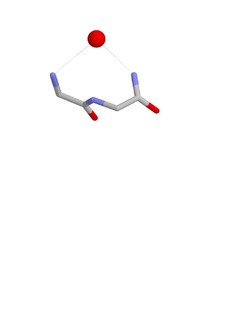
The Nest is a type of protein structural motif. It is a small recurring anion-binding feature of both proteins and peptides. Each consists of the main chain atoms of three consecutive amino acid residues. The main chain NH groups bind the anions while the side chain atoms are often not involved. Proline residues lack NH groups so are rare in nests. About one in 12 of amino acid residues in proteins, on average, belongs to a nest.

GeNMR method is the first fully automated template-based method of protein structure determination that utilizes both NMR chemical shifts and NOE -based distance restraints.

Volume, Area, Dihedral Angle Reporter (VADAR) is a freely available protein structure validation web server that was developed as a collaboration between Dr. Brian Sykes and Dr. David Wishart at the University of Alberta. VADAR consists of >15 different algorithms and programs for assessing and validating peptide and protein structures from their PDB coordinate data. VADAR is capable of determining secondary structure, identifying and classifying six different types of beta turns, determining and calculating the strength of C=O -- N-H hydrogen bonds, calculating residue-specific accessible surface areas (ASA), calculating residue volumes, determining backbone and side chain torsion angles, assessing local structure quality, evaluating global structure quality and identifying residue “outliers”. The results have been validated through extensive comparison to published data and careful visual inspection. VADAR produces both text and graphical output with most of the quantitative data presented in easily viewed tables. In particular, VADAR’s output is presented in a vertical, tabular format with most of the sequence data, residue numbering and any other calculated property or feature presented from top to bottom, rather than from left to right.

References

1 2 Kolodny, R., Guibas, L., Levitt, M., and Koehl, P. (2005, March). Inverse Kinematics in Biology: The Protein Loop Closure Problem. The International Journal of Robotics Research 24(2-3), 151-163.
1 2 Simons, K., Kooperberg, C., Huang, E., and Baker, D. (1997). Assembly of Protein Tertiary Structures from Fragments with Similar Local Sequences using Simulated Annealing and Bayesian Scoring Functions. J Mol Biol 268, 209-225.
↑ Bujnicki, J. (2006) Protein Structure Prediction by Recombination of Fragments. ChemBioChem. 7, 19-27.
↑ Li, S. et al. (2008) Fragment-HMM: A New Approach to Protein Structure Prediction. Protein Science. 17, 1925-1934.
↑ DiMaio, F., Shavlik, J., Phillips, G. A probabilistic approach to protein backbone tracing in electron density maps (2006). Bioinformatics 22(14), 81-89.
↑ Canutescu, A., Shelenkov, A., and Dunbrack, R. (2003). A graph theory algorithm for protein side-chain prediction. Protein Sci. 12, 2001–2014.
1 2 Kolodny, R., Koehl, P., Guibas, L., and Levitt, M. (2005). Small Libraries of Protein Fragments Model Native Protein Structures Accurately. J Mol Biol 323, 297-307.
↑ Du, P., Andrec, M., and Levy, R. Have We Seen All Structures Corresponding to Short Protein Fragments in the Protein Data Bank? An Update. Protein Engineering. 2003, 16(6) 407-414.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[KolodnyLoop-1] 1 2 Kolodny, R., Guibas, L., Levitt, M., and Koehl, P. (2005, March). Inverse Kinematics in Biology: The Protein Loop Closure Problem. The International Journal of Robotics Research 24(2-3), 151-163.

[Baker1997-2] 1 2 Simons, K., Kooperberg, C., Huang, E., and Baker, D. (1997). Assembly of Protein Tertiary Structures from Fragments with Similar Local Sequences using Simulated Annealing and Bayesian Scoring Functions. J Mol Biol 268, 209-225.

[Bujnicki-3] Bujnicki, J. (2006) Protein Structure Prediction by Recombination of Fragments. ChemBioChem. 7, 19-27.

[LiFragmentHMM-4] Li, S. et al. (2008) Fragment-HMM: A New Approach to Protein Structure Prediction. Protein Science. 17, 1925-1934.

[DiMaio-5] DiMaio, F., Shavlik, J., Phillips, G. A probabilistic approach to protein backbone tracing in electron density maps (2006). Bioinformatics 22(14), 81-89.

[dunbrackLib-6] Canutescu, A., Shelenkov, A., and Dunbrack, R. (2003). A graph theory algorithm for protein side-chain prediction. Protein Sci. 12, 2001–2014.

[KolodnyLibrary-7] 1 2 Kolodny, R., Koehl, P., Guibas, L., and Levitt, M. (2005). Small Libraries of Protein Fragments Model Native Protein Structures Accurately. J Mol Biol 323, 297-307.

[DuAllFragments-8] Du, P., Andrec, M., and Levy, R. Have We Seen All Structures Corresponding to Short Protein Fragments in the Protein Data Bank? An Update. Protein Engineering. 2003, 16(6) 407-414.