Pythagoras number

Last updated August 25, 2024

In mathematics, the Pythagoras number or reduced height of a field describes the structure of the set of squares in the field. The Pythagoras number p(K) of a field K is the smallest positive integer p such that every sum of squares in K is a sum of p squares.

Examples

Every non-negative real number is a square, so p(R) = 1.
For a finite field of odd characteristic, not every element is a square, but all are the sum of two squares,^[1] so p = 2.
By Lagrange's four-square theorem, every positive rational number is a sum of four squares, and not all are sums of three squares, so p(Q) = 4.

Properties

Every positive integer occurs as the Pythagoras number of some formally real field.^[2]
The Pythagoras number is related to the Stufe by p(F) ≤ s(F) + 1.^[3] If F is not formally real then s(F) ≤ p(F) ≤ s(F) + 1,^[4] and both cases are possible: for F = C we have s = p = 1, whereas for F = F₅ we have s = 1, p = 2.^[5]
As a consequence, the Pythagoras number of a non-formally-real field is either a power of 2, or 1 more than a power of 2. All such cases occur: i.e., for each pair (s,p) of the form (2^k,2^k) or (2^k,2^k + 1), there exists a field F such that (s(F),p(F)) = (s,p).^[6] For example, quadratically closed fields (e.g., C) and fields of characteristic 2 (e.g., F₂) give (s(F),p(F)) = (1,1); for primes p ≡ 1 (mod 4), F_p and the p-adic field Q_p give (1,2); for primes p ≡ 3 (mod 4), F_p gives (2,2), and Q_p gives (2,3); Q₂ gives (4,4), and the function field Q₂(X) gives (4,5).
The Pythagoras number is related to the height of a field F: if F is formally real then h(F) is the smallest power of 2 which is not less than p(F); if F is not formally real then h(F) = 2s(F).^[7]

Notes

↑ Lam (2005) p. 36
↑ Lam (2005) p. 398
↑ Rajwade (1993) p. 44
↑ Rajwade (1993) p. 228
↑ Rajwade (1993) p. 261
↑ Lam (2005) p. 396
↑ Lam (2005) p. 395

Related Research Articles

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.

In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Basic examples of ordered fields are the rational numbers and the real numbers, both with their standard orderings.

<span class="mw-page-title-main">Factorization</span> (Mathematical) decomposition into a product

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, $3 \times 5$ is an integer factorization of $15$ , and $(x - 2)(x + 2)$ is a polynomial factorization of $x 2 - 4$ .

In mathematics, a field K is called a non-Archimedean local field if it is complete with respect to a metric induced by a discrete valuation v and if its residue field k is finite. In general, a local field is a locally compact topological field with respect to a non-discrete topology. The real numbers R, and the complex numbers C are Archimedean local fields. Given a local field, the valuation defined on it can be of either of two types, each one corresponds to one of the two basic types of local fields: those in which the valuation is Archimedean and those in which it is not. In the first case, one calls the local field an Archimedean local field, in the second case, one calls it a non-Archimedean local field. Local fields arise naturally in number theory as completions of global fields.

In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,

Field theory is the branch of mathematics in which fields are studied. This is a glossary of some terms of the subject.

In mathematics, the ring of integers of an algebraic number field $is the ring of all algebraic integers contained in . An algebraic integer is a root of a monic polynomial with integer coefficients: . This ring is often denoted by or . Since any integer belongs to and is an integral element of, the ring is always a subring of .$

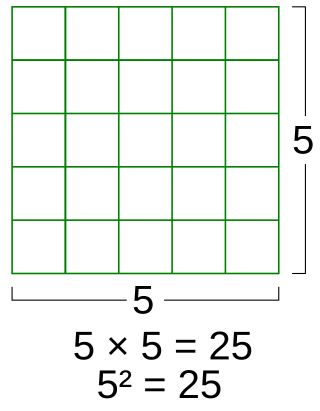
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 3², which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x². The adjective which corresponds to squaring is quadratic.

In mathematics, in particular in field theory and real algebra, a formally real field is a field that can be equipped with a ordering that makes it an ordered field.

<span class="mw-page-title-main">Hasse–Minkowski theorem</span> Two quadratic forms over a number field are equivalent iff they are equivalent locally

The Hasse–Minkowski theorem is a fundamental result in number theory which states that two quadratic forms over a number field are equivalent if and only if they are equivalent locally at all places, i.e. equivalent over every topological completion of the field. A related result is that a quadratic space over a number field is isotropic if and only if it is isotropic locally everywhere, or equivalently, that a quadratic form over a number field nontrivially represents zero if and only if this holds for all completions of the field. The theorem was proved in the case of the field of rational numbers by Hermann Minkowski and generalized to number fields by Helmut Hasse. The same statement holds even more generally for all global fields.

Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It concerns the expression of positive definite rational functions as sums of quotients of squares. The original question may be reformulated as:

In mathematics, a universal quadratic form is a quadratic form over a ring that represents every element of the ring. A non-singular form over a field which represents zero non-trivially is universal.

In mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.

In mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which the form evaluates to zero. Otherwise it is a definite quadratic form. More explicitly, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be isotropic if q(v) = 0. A quadratic form is isotropic if and only if there exists a non-zero isotropic vector (or null vector) for that quadratic form.

Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Part of the inspiration comes from complex dynamics, the study of the iteration of self-maps of the complex plane or other complex algebraic varieties. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, $p$ -adic, or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.

In algebra, a Pythagorean field is a field in which every sum of two squares is a square: equivalently it has Pythagoras number equal to 1. A Pythagorean extension of a field $is an extension obtained by adjoining an element for some in . So a Pythagorean field is one closed under taking Pythagorean extensions. For any field there is a minimal Pythagorean field containing it, unique up to isomorphism, called its Pythagorean closure . The Hilbert field is the minimal ordered Pythagorean field.$

In field theory, a branch of mathematics, the Stufe (/ʃtuːfə/; German: level) s(F) of a field F is the least number of squares that sum to −1. If −1 cannot be written as a sum of squares, s(F) = $. In this case, F is a formally real field. Albrecht Pfister proved that the Stufe, if finite, is always a power of 2, and that conversely every power of 2 occurs.$

In mathematics, the universal invariant or u-invariant of a field describes the structure of quadratic forms over the field.

In mathematics, a quadratically closed field is a field of characteristic not equal to 2 in which every element has a square root.

In mathematics, the Hurwitz problem is the problem of finding multiplicative relations between quadratic forms which generalise those known to exist between sums of squares in certain numbers of variables.

References

Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics. Vol. 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.
Rajwade, A. R. (1993). Squares. London Mathematical Society Lecture Note Series. Vol. 171. Cambridge University Press. ISBN 0-521-42668-5. Zbl 0785.11022.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Lam36-1] Lam (2005) p. 36

[Lam398-2] Lam (2005) p. 398

[R44-3] Rajwade (1993) p. 44

[R228-4] Rajwade (1993) p. 228

[R261-5] Rajwade (1993) p. 261

[Lam396-6] Lam (2005) p. 396

[Lam395-7] Lam (2005) p. 395

[1]

[2]

[3]

[4]

[5]

[6]

[7]