In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on the real line or by Fourier series for periodic functions. Generalizing these transforms to other domains is generally called Fourier analysis, although the term is sometimes used interchangeably with harmonic analysis. Harmonic Analysis has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis and neuroscience.

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.

In dynamical systems theory and control theory, a phase space or state space is a space in which all possible "states" of a dynamical system or a control system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.

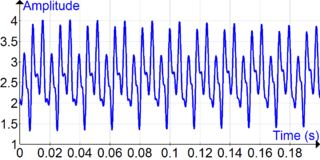
A sine wave, sinusoidal wave, or sinusoid is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is simple harmonic motion; as rotation, it corresponds to uniform circular motion. Sine waves occur often in physics, including wind waves, sound waves, and light waves. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies.
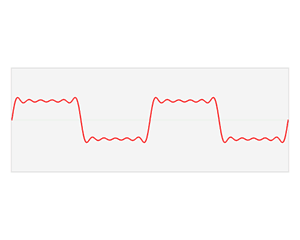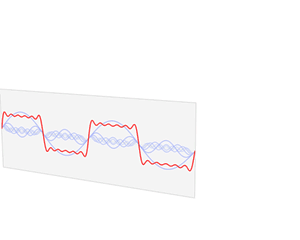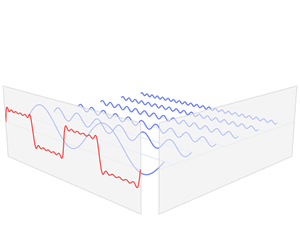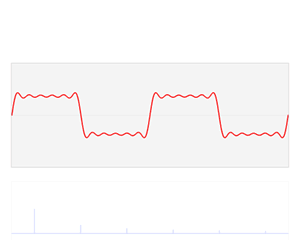
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signal changes over time, whereas a frequency-domain graph shows how the signal is distributed within different frequency bands over a range of frequencies. A frequency-domain representation consists of both the magnitude and the phase of a set of sinusoids at the frequency components of the signal. Although it is common to refer to the magnitude portion as the frequency response of a signal, the phase portion is required to uniquely define the signal.
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone–von Neumann theorem and canonical commutation relations for details.
A time–frequency representation (TFR) is a view of a signal represented over both time and frequency. Time–frequency analysis means analysis into the time–frequency domain provided by a TFR. This is achieved by using a formulation often called "Time–Frequency Distribution", abbreviated as TFD.
In mathematics, in the area of harmonic analysis, the fractional Fourier transform (FRFT) is a family of linear transformations generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power, where n need not be an integer — thus, it can transform a function to any intermediate domain between time and frequency. Its applications range from filter design and signal analysis to phase retrieval and pattern recognition.

The Wigner quasiprobability distribution is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space.
In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms. It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). As this defines the original function up to a sign, this translates into an action of its double cover on the original function space.

Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum based on a least-squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in the long and gapped records; LSSA mitigates such problems. Unlike in Fourier analysis, data need not be equally spaced to use LSSA.
The Mehler kernel is a complex-valued function found to be the propagator of the quantum harmonic oscillator.

Maurice A. de Gosson, is an Austrian mathematician and mathematical physicist, born in 1948 in Berlin. He is currently a Senior Researcher at the Numerical Harmonic Analysis Group (NuHAG) of the University of Vienna.
In physics and geometry, there are two closely related vector spaces, usually three-dimensional but in general of any finite dimension. Position space is the set of all position vectorsr in Euclidean space, and has dimensions of length; a position vector defines a point in space. Momentum space is the set of all momentum vectorsp a physical system can have; the momentum vector of a particle corresponds to its motion, with units of [mass][length][time]−1.








