Quaternionic projective space

Last updated June 06, 2023

In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions $\mathbb {H} .$ Quaternionic projective space of dimension n is usually denoted by

In coordinates

Its direct construction is as a special case of the projective space over a division algebra. The homogeneous coordinates of a point can be written

[q_{0},q_{1},\ldots ,q_{n}]

where the $q_{i}$ are quaternions, not all zero. Two sets of coordinates represent the same point if they are 'proportional' by a left multiplication by a non-zero quaternion c; that is, we identify all the

[cq_{0},cq_{1}\ldots ,cq_{n}]

.

In the language of group actions, $\mathbb {HP} ^{n}$ is the orbit space of $\mathbb {H} ^{n+1}\setminus \{(0,\ldots ,0)\}$ by the action of $\mathbb {H} ^{\times }$ , the multiplicative group of non-zero quaternions. By first projecting onto the unit sphere inside $\mathbb {H} ^{n+1}$ one may also regard $\mathbb {HP} ^{n}$ as the orbit space of $S^{4n+3}$ by the action of ${\text{Sp}}(1)$ , the group of unit quaternions.^[1] The sphere $S^{4n+3}$ then becomes a principal Sp(1)-bundle over $\mathbb {HP} ^{n}$ :

\mathrm {Sp} (1)\to S^{4n+3}\to \mathbb {HP} ^{n}.

This bundle is sometimes called a (generalized) Hopf fibration.

There is also a construction of $\mathbb {HP} ^{n}$ by means of two-dimensional complex subspaces of $\mathbb {H} ^{2n}$ , meaning that $\mathbb {HP} ^{n}$ lies inside a complex Grassmannian.

Topology

Homotopy theory

The space $\mathbb {HP} ^{\infty }$ , defined as the union of all finite $\mathbb {HP} ^{n}$ 's under inclusion, is the classifying space BS³. The homotopy groups of $\mathbb {HP} ^{\infty }$ are given by $\pi _{i}(\mathbb {HP} ^{\infty })=\pi _{i}(BS^{3})\cong \pi _{i-1}(S^{3}).$ These groups are known to be very complex and in particular they are non-zero for infinitely many values of $i$ . However, we do have that

\pi _{i}(\mathbb {HP} ^{\infty })\otimes \mathbb {Q} \cong {\begin{cases}\mathbb {Q} &i=4\\0&i\neq 4\end{cases}}

It follows that rationally, i.e. after localisation of a space, $\mathbb {HP} ^{\infty }$ is an Eilenberg–Maclane space $K(\mathbb {Q} ,4)$ . That is $\mathbb {HP} _{\mathbb {Q} }^{\infty }\simeq K(\mathbb {Z} ,4)_{\mathbb {Q} }.$ (cf. the example K(Z,2)). See rational homotopy theory.

In general, $\mathbb {HP} ^{n}$ has a cell structure with one cell in each dimension which is a multiple of 4, up to $4n$ . Accordingly, its cohomology ring is $\mathbb {Z} [v]/v^{n+1}$ , where $v$ is a 4-dimensional generator. This is analogous to complex projective space. It also follows from rational homotopy theory that $\mathbb {HP} ^{n}$ has infinite homotopy groups only in dimensions 4 and $4n+3$ .

Differential geometry

$\mathbb {HP} ^{n}$ carries a natural Riemannian metric analogous to the Fubini-Study metric on $\mathbb {CP} ^{n}$ , with respect to which it is a compact quaternion-Kähler symmetric space with positive curvature.

Quaternionic projective space can be represented as the coset space

\mathbb {HP} ^{n}=\operatorname {Sp} (n+1)/\operatorname {Sp} (n)\times \operatorname {Sp} (1)

where $\operatorname {Sp} (n)$ is the compact symplectic group.

Characteristic classes

Since $\mathbb {HP} ^{1}=S^{4}$ , its tangent bundle is stably trivial. The tangent bundles of the rest have nontrivial Stiefel–Whitney and Pontryagin classes. The total classes are given by the following formulas:

w(\mathbb {HP} ^{n})=(1+u)^{n+1}

p(\mathbb {HP} ^{n})=(1+v)^{2n+2}(1+4v)^{-1}

where $v$ is the generator of $H^{4}(\mathbb {HP} ^{n};\mathbb {Z} )$ and $u$ is its reduction mod 2.^[2]

Special cases

Quaternionic projective line

The one-dimensional projective space over $\mathbb {H}$ is called the "projective line" in generalization of the complex projective line. For example, it was used (implicitly) in 1947 by P. G. Gormley to extend the Möbius group to the quaternion context with linear fractional transformations. For the linear fractional transformations of an associative ring with 1, see projective line over a ring and the homography group GL(2,A).

From the topological point of view the quaternionic projective line is the 4-sphere, and in fact these are diffeomorphic manifolds. The fibration mentioned previously is from the 7-sphere, and is an example of a Hopf fibration.

Explicit expressions for coordinates for the 4-sphere can be found in the article on the Fubini–Study metric.

Quaternionic projective plane

The 8-dimensional $\mathbb {HP} ^{2}$ has a circle action, by the group of complex scalars of absolute value 1 acting on the other side (so on the right, as the convention for the action of c above is on the left). Therefore, the quotient manifold

\mathbb {HP} ^{2}/\mathrm {U} (1)

may be taken, writing U(1) for the circle group. It has been shown that this quotient is the 7-sphere, a result of Vladimir Arnold from 1996, later rediscovered by Edward Witten and Michael Atiyah.

Related Research Articles

<span class="mw-page-title-main">3-sphere</span> Mathematical object

In mathematics, a 3-sphere, glome or hypersphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

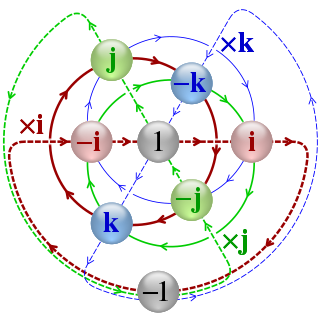
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.

In mathematics, the orthogonal group in dimension $, denoted, is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.$

In mathematics, the special unitary group of degree $n$ , denoted $SU(n)$ , is the Lie group of $n \times n$ unitary matrices with determinant 1.

In mathematics the spin group Spin(n) is a Lie group whose underlying manifold is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups (when n ≠ 2)

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the $3$ -sphere onto the $2$ -sphere such that each distinct point of the $2$ -sphere is mapped from a distinct great circle of the $3$ -sphere. Thus the $3$ -sphere is composed of fibers, where each fiber is a circle — one for each point of the $2$ -sphere.

In differential geometry, a hyperkähler manifold is a Riemannian manifold $endowed with three integrable almost complex structures that are Kähler with respect to the Riemannian metric and satisfy the quaternionic relations . In particular, it is a hypercomplex manifold. All hyperkähler manifolds are Ricci-flat and are thus Calabi-Yau manifolds.$

In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines through the origin of a complex Euclidean space (see below for an intuitive account). Formally, a complex projective space is the space of complex lines through the origin of an (n+1)-dimensional complex vector space. The space is denoted variously as P(Cⁿ⁺¹), P_n(C) or CPⁿ. When n = 1, the complex projective space CP¹ is the Riemann sphere, and when n = 2, CP² is the complex projective plane (see there for a more elementary discussion).

In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by Raoul Bott, which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy groups of spheres. Bott periodicity can be formulated in numerous ways, with the periodicity in question always appearing as a period-2 phenomenon, with respect to dimension, for the theory associated to the unitary group. See for example topological K-theory.

In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.

In mathematics, specifically in homotopy theory, a classifying spaceBG of a topological group G is the quotient of a weakly contractible space EG by a proper free action of G. It has the property that any G principal bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle EG → BG. As explained later, this means that classifying spaces represent a set-valued functor on the homotopy category of topological spaces. The term classifying space can also be used for spaces that represent a set-valued functor on the category of topological spaces, such as Sierpiński space. This notion is generalized by the notion of classifying topos. However, the rest of this article discusses the more commonly used notion of classifying space up to homotopy.

In mathematics, real projective space, denoted $or is the topological space of lines passing through the origin 0 in the real space It is a compact, smooth manifold of dimension n, and is a special case of a Grassmannian space.$

In mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories derived from it, such as Brown–Peterson cohomology or Morava K-theory, that are easier to compute.

In mathematics, specifically algebraic topology, an Eilenberg–MacLane space is a topological space with a single nontrivial homotopy group.

In differential geometry, a quaternion-Kähler manifold (or quaternionic Kähler manifold) is a Riemannian 4n-manifold whose Riemannian holonomy group is a subgroup of Sp(n)·Sp(1) for some $. Here Sp(n) is the sub-group of consisting of those orthogonal transformations that arise by left -multiplication by some quaternionic matrix, while the group of unit-length quaternions instead acts on quaternionic -space by right scalar multiplication. The Lie group generated by combining these actions is then abstractly isomorphic to .$

In differential geometry, a hypercomplex manifold is a manifold with the tangent bundle equipped with an action by the algebra of quaternions in such a way that the quaternions $define integrable almost complex structures.$

<span class="mw-page-title-main">Classical group</span>

In mathematics, the classical groups are defined as the special linear groups over the reals $R$ , the complex numbers $C$ and the quaternions $H$ together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph The Classical Groups.

In algebraic geometry, given a smooth projective curve X over a finite field $and a smooth affine group scheme G over it, the moduli stack of principal bundles over X, denoted by, is an algebraic stack given by: for any -algebra R,$

This is a glossary of properties and concepts in algebraic topology in mathematics.

In differential geometry, a quaternionic manifold is a quaternionic analog of a complex manifold. The definition is more complicated and technical than the one for complex manifolds due in part to the noncommutativity of the quaternions and in part to the lack of a suitable calculus of holomorphic functions for quaternions. The most succinct definition uses the language of G-structures on a manifold. Specifically, a quaternionic n-manifold can be defined as a smooth manifold of real dimension 4n equipped with a torsion-free $-structure. More naïve, but straightforward, definitions lead to a dearth of examples, and exclude spaces like quaternionic projective space which should clearly be considered as quaternionic manifolds.$

References

↑ Naber, Gregory L. (2011) [1997]. "Physical and Geometrical Motivation". Topology, Geometry and Gauge fields. Texts in Applied Mathematics. Vol. 25. Springer. p. 50. doi:10.1007/978-1-4419-7254-5_0. ISBN 978-1-4419-7254-5.
↑ Szczarba, R.H. (1964). "On tangent bundles of fibre spaces and quotient spaces" (PDF). American Journal of Mathematics. 86 (4): 685–697. doi:10.2307/2373152. JSTOR 2373152.