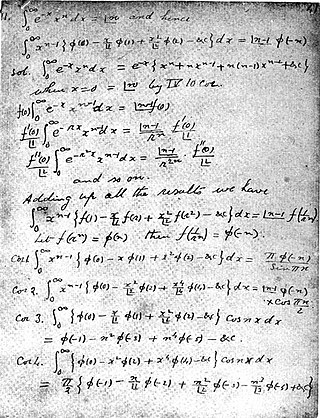The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

In mathematics, the Bernoulli polynomials, named after Jacob Bernoulli, combine the Bernoulli numbers and binomial coefficients. They are used for series expansion of functions, and with the Euler–MacLaurin formula.

In mathematics, the Clausen function, introduced by Thomas Clausen, is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.

In mathematics, the polygamma function of order m is a meromorphic function on the complex numbers defined as the (m + 1)th derivative of the logarithm of the gamma function:

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, … by

In number theory, the Mertens function is defined for all positive integers n as

In mathematics, in the area of analytic number theory, the Dirichlet eta function is defined by the following Dirichlet series, which converges for any complex number having real part > 0:
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.

In mathematics, the Dirichlet beta function is a special function, closely related to the Riemann zeta function. It is a particular Dirichlet L-function, the L-function for the alternating character of period four.
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation
In number theory, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula
In mathematics, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function. For the explicit case of the gamma function, the identity is a product of values; thus the name. The various relations all stem from the same underlying principle; that is, the relation for one special function can be derived from that for the others, and is simply a manifestation of the same identity in different guises.
In statistics, the generalized Marcum Q-function of order is defined as
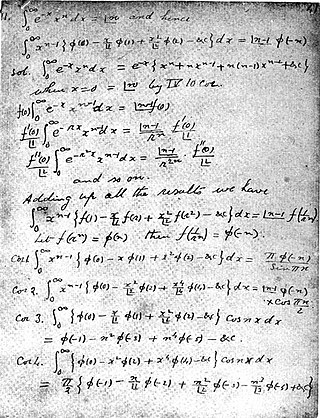
In mathematics, Ramanujan's Master Theorem, named after Srinivasa Ramanujan, is a technique that provides an analytic expression for the Mellin transform of an analytic function.
The Bernoulli polynomials of the second kindψn(x), also known as the Fontana–Bessel polynomials, are the polynomials defined by the following generating function: