In graph theory, the rectilinear minimum spanning tree (RMST) of a set of n points in the plane (or more generally, in ) is a minimum spanning tree of that set, where the weight of the edge between each pair of points is the rectilinear distance between those two points.
By explicitly constructing the complete graph on n vertices, which has n(n-1)/2 edges, a rectilinear minimum spanning tree can be found using existing algorithms for finding a minimum spanning tree. In particular, using Prim's algorithm with an adjacency matrix yields time complexity O(n2).
In the planar case, more efficient algorithms exist. They are based on the idea that connections may only happen with the nearest neighbour of a point in each octant - that is, each of the eight regions of the plane delimited by the coordinate axis from this point and their bisectors.
The resulting graph has only a linear number of edges and can be constructed in O(n log n) using a divide and conquer algorithm [1] or a sweep line algorithm. [2]
The problem commonly arises in physical design of electronic circuits. In modern high-density integrated circuits wire routing is performed by wires which consist of segments running horizontally in one layer of metal and vertically in another metal layer. As a result, the wire length between two points is naturally measured with rectilinear distance. Although the routing of a whole net with multiple nodes is better represented by the rectilinear Steiner tree, the RMST provides a reasonable approximation and wire length estimate. [3]
The travelling salesman problem, also known as the travelling salesperson problem (TSP), asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
Kruskal's algorithm finds a minimum spanning forest of an undirected edge-weighted graph. If the graph is connected, it finds a minimum spanning tree. It is a greedy algorithm that in each step adds to the forest the lowest-weight edge that will not form a cycle. The key steps of the algorithm are sorting and the use of a disjoint-set data structure to detect cycles. Its running time is dominated by the time to sort all of the graph edges by their weight.
Borůvka's algorithm is a greedy algorithm for finding a minimum spanning tree in a graph, or a minimum spanning forest in the case of a graph that is not connected.
In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.
In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals and minimizes the total weight of its edges. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.
A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
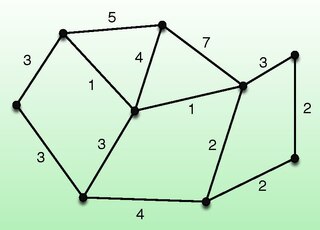
The k-minimum spanning tree problem, studied in theoretical computer science, asks for a tree of minimum cost that has exactly k vertices and forms a subgraph of a larger graph. It is also called the k-MST or edge-weighted k-cardinality tree. Finding this tree is NP-hard, but it can be approximated to within a constant approximation ratio in polynomial time.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.
The nearest neighbor graph (NNG) is a directed graph defined for a set of points in a metric space, such as the Euclidean distance in the plane. The NNG has a vertex for each point, and a directed edge from p to q whenever q is a nearest neighbor of p, a point whose distance from p is minimum among all the given points other than p itself.
In geometry, the Hanan gridH(S) of a finite set S of points in the plane is obtained by constructing vertical and horizontal lines through each point in S.
In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points and by an edge whenever there does not exist a third point that is closer to both and than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.
In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.
The rectilinear Steiner tree problem, minimum rectilinear Steiner tree problem (MRST), or rectilinear Steiner minimum tree problem (RSMT) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance is replaced with the rectilinear distance. The problem may be formally stated as follows: given n points in the plane, it is required to interconnect them all by a shortest network which consists only of vertical and horizontal line segments. It can be shown that such a network is a tree whose vertices are the input points plus some extra points.
In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
In the theory of cluster analysis, the nearest-neighbor chain algorithm is an algorithm that can speed up several methods for agglomerative hierarchical clustering. These are methods that take a collection of points as input, and create a hierarchy of clusters of points by repeatedly merging pairs of smaller clusters to form larger clusters. The clustering methods that the nearest-neighbor chain algorithm can be used for include Ward's method, complete-linkage clustering, and single-linkage clustering; these all work by repeatedly merging the closest two clusters but use different definitions of the distance between clusters. The cluster distances for which the nearest-neighbor chain algorithm works are called reducible and are characterized by a simple inequality among certain cluster distances.
In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.
In computational geometry, a greedy geometric spanner is an undirected graph whose distances approximate the Euclidean distances among a finite set of points in a Euclidean space. The vertices of the graph represent these points. The edges of the spanner are selected by a greedy algorithm that includes an edge whenever its two endpoints are not connected by a short path of shorter edges. The greedy spanner was first described in the PhD thesis of Gautam Das and conference paper and subsequent journal paper by Ingo Althöfer et al. These sources also credited Marshall Bern (unpublished) with the independent discovery of the same construction.
