Reversibly assembled cellular composite materials

Last updated

Reversibly assembled cellular composite materials (RCCM) are three-dimensional lattices of modular structures that can be partially disassembled to enable repairs or other modifications. Each cell incorporates structural material and a reversible interlock, allowing lattices of arbitrary size and shape. RCCM display three-dimensional symmetry derived from the geometry as linked. [1] [2]

Contents

The discrete construction of reversibly assembled cellular composites introduces a new degree of freedom that determines global functional properties from the local placement of heterogeneous components. Because the individual parts are literally finite elements, a hierarchical decomposition describes the part types and their combination in a structure. [1]

RCCM can be viewed as a "digital" material in which discrete parts link with a discrete set of relative positions and orientations. An assembler can place them using only local information. Placement errors can be detected and corrected by assembly reversal. These materials combine the size and strength of composites with the low density of cellular materials and the convenience of additive manufacturing. [1]

History

RCCM were introduced in 2013 by researchers at the MIT Center for Bits and Atoms. [2]

Behavior

Elasticity

RCCM lattices behave as an elastic solid in both tension and compression. They offer both a linear regime and a nonlinear super-elastic deformation mode a modulus an order of magnitude greater than for an ultralight material (12.3 megapascals at a density of 7.2 mg per cubic centimeter). Bulk properties can be predicted from component measurements and deformation modes determined by the placement of part types. Site locations are locally constrained, yielding structures that merge desirable features of carbon fiber composites, cellular materials and additive manufacturing. [1]

Nonlinear elastic behavior derives from a multi-axial elastic instability of the lattice, a complex coordinated elastic buckling of the strut members. The resulting geometry is similar to a Jahn–Teller distortion of an octahedral complex with respect to orientation about the octahedral centers. Elastic folding or pleating can occur in three dimensions, likely a coordinated antisymmetric twisting stress response and/or plastic deformation. [1] [3]

Failure

Unlike conventional composites, which typically fail catastrophically, RCCM fail incrementally because of the non-linear deformation phase and the multiplicity of joints and links. These results matched finite-element simulations [4] with finely-meshed rigid body models. In addition to convergence to the observed coordinated buckling mode, these simulations accurately predict the relative strength scaling observed in load test experiments. These results are consistent with the observation that open-cell lattice materials fail through micro-structural strut bending failures with σmax ∝. The simulations also suggest that the coordinated buckling phenomenon as well as the modulus measurements are not dominated by edge effects, with minimal influence on overall results beyond characteristic lengths exceeding several units. [1]

Varying the locations of more and less rigid elements can trigger pure axial compression, simple uni-directional Euler buckling and complex buckling. [1] [3]

Scaling

Cellular composites extend stretch-dominated lattices to the ultralight regime (below ten milligrams per cubic centimeter). Performance depends positively on the framework rigidity of the lattice, node connectivity, slenderness of strut members and the scaling of the density cost of mechanical connections. [1]

Conventional fiber composites make truss cores and structural frames, with bonded assembly of substructures or continuous fiber winding. Examples of such truss cores have been reported with continuous two-dimensional (2D) geometric symmetry and nearly ideal but highly anisotropic specific modulus scaling.

Three-dimensional open-cell lattice materials occur in natural and engineered systems, spanning many length scales. Their mechanical properties scale with relative density according to the geometry. They display either stretch-dominated or transverse beam bending-dominated microstructural behavior, based on periodic mechanical models. For Young’s modulus E, ideal stretch-dominated scaling with density ρ follows a proportional law E∝ρ, while common stochastic foams follow a quadratic law E∝ρ2 otherwise associated with transverse beam bending-dominated behavior. At ultralight densities a further reduced cubic scaling law E∝ρ3 is common, such as with aerogels and aerogel composites. [1]

The dependence of scaling on geometry is seen in periodic lattice-based materials that have nearly ideal E∝ρ scaling, with high node connectedness relative to stochastic foams. These structures have previously been implemented only in relatively dense engineered materials. For the ultralight regime the E∝ρ2 scaling seen in denser stochastic cellular materials applies to electroplated tubular nickel micro-lattices, as well as carbon-based open-cell stochastic foams, including carbon microtube aerographite and graphene cork. [1]

Design

Making the connections stiffer and stronger than the strut members means that stress response is governed by the struts. [3] Extending dimensional scaling methods to include the connections shows that the mass density cost of robust connections – which scale with the strut's cross-sectional area – is low for ultralight materials, where strut diameter dominates mass density scaling. The relative density (ρ/ρs) of these materials is the sum of the relative density contribution of the strut members (ρm/ρs) and the relative density contribution of the connections (ρc/ρs). The strut members have a thickness t and length L. The connections transfer forces through load-bearing surface contacts, requiring that the characteristic dimensions of the connections scale with the cross section of the attached strut members, t2, because this dimension determines the maximum stress transferable through the joint. [1]

These definitions give a cubic scaling relation between the relative mass contribution of the joints and the strut's thickness-to-length ratio (ρc/ρs ∝ Cc(t/L)3, where Cc is the connection contribution constant determined by the lattice geometry). The struts' relative density contribution scales quadratically with the thickness-to-length ratio of the struts (ρm/ρs ∝ Cm (t/L)2), which agrees with the literature on classical cellular materials. Mechanical properties (such as modulus and strength) scale with overall relative density, which in turn scales primarily with the strut and not the connection, considering only open cell lattices with slender struts [t/L < 0.1 (7)], given that the geometric constants Cc and Cm are of the same order of magnitude [ρ/ρs ∝ Cc (t/L)3 + Cm (t/L)2]. [3] The density cost of the mechanical joints decreases with increasing strut member slenderness (decreasing t/L) and decreasing relative density. [1]

Tiling the cross-shaped parts forms the lattice structure. Each part contributes four conjoined strut members to one locally central node and one strut to four peripheral nodes. A shear clip inserted through the four coincident connection holes links the cells. [1]

Each cell includes aligned fiber composite beams and looped fiber load-bearing holes that reversibly chain together to form volume-filling lattices. Mass-produced cells can be assembled to fill arbitrary structural shapes, with a resolution prescribed by the part scale that matches the variability of an application's boundary stress. The periodic nature of assemblies simplifies behavior analysis and prediction. [1]

Cuboct geometry

A “cuboct” cubic lattice of vertex connected octahedrons, similar to the perovskite mineral structure provides a regular polyhedral unit cell that satisfies Maxwell’s rigidity criterion and has a coordination number z of eight. The dependence of the relative density on the coordination number is small relative to the dependence on strut diameter. Winding the reinforcing fibers around the connection holes optimizes their load bearing capacity, while coupling them to struts which themselves retain uniaxial fiber orientation. [1]

Comparison with traditional composite materials

Carbon-fiber reinforced composite materials can improve efficiency in engineered systems (for example, airframes) by reducing structural weight for given strength and stiffness requirements, but present challenges with manufacturing and certification. High-performance composite components employ many continuous fibers that span the shape of a component, and are embedded in a resin matrix. Such parts typically require custom tooling, pressurization for consolidation and heated curing. Joining such parts adds complexity and structural vulnerabilities. [1]

RCCM eliminate the need for custom tooling because parts can be incrementally added/removed. Their construction, modification, repair and re-use can all employ the same reversible linking process. Heterogeneous elements can be incorporated in structures with functions determined by their relative placement. Exact assembly of discrete cellular composites offers new properties and performance not available with the analog alternatives of continuously depositing or removing material. [1]

Related Research Articles

<span class="mw-page-title-main">Anisotropy</span> In geometry, property of being directionally dependent

Anisotropy is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit very different properties when measured along different axes: physical or mechanical properties.

<i>Luffa</i> Genus of vines

Luffa is a genus of tropical and subtropical vines in the pumpkin, squash and gourd family (Cucurbitaceae).

<span class="mw-page-title-main">Composite material</span> Material made from a combination of two or more unlike substances

A composite material is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions.

<span class="mw-page-title-main">Foam</span> Form of matter

Foams are materials formed by trapping pockets of gas in a liquid or solid.

In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to plasticity, in which the object fails to do so and instead remains in its deformed state.

<span class="mw-page-title-main">Trabecula</span> Tissue element that supports or anchors a framework of parts within a body or organ

A trabecula is a small, often microscopic, tissue element in the form of a small beam, strut or rod that supports or anchors a framework of parts within a body or organ. A trabecula generally has a mechanical function, and is usually composed of dense collagenous tissue. It can be composed of other material such as muscle and bone. In the heart, muscles form trabeculae carneae and septomarginal trabeculae. Cancellous bone is formed from groupings of trabeculated bone tissue.

<span class="mw-page-title-main">Work hardening</span> Strengthening a material through plastic deformation

In materials science, work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.

Specific modulus is a materials property consisting of the elastic modulus per mass density of a material. It is also known as the stiffness to weight ratio or specific stiffness. High specific modulus materials find wide application in aerospace applications where minimum structural weight is required. The dimensional analysis yields units of distance squared per time squared. The equation can be written as:

<span class="mw-page-title-main">Yield (engineering)</span> Phenomenon of deformation due to structural stress

In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation.

<span class="mw-page-title-main">Honeycomb structure</span> Natural or man-made structures that have the geometry of a honeycomb

Honeycomb structures are natural or man-made structures that have the geometry of a honeycomb to allow the minimization of the amount of used material to reach minimal weight and minimal material cost. The geometry of honeycomb structures can vary widely but the common feature of all such structures is an array of hollow cells formed between thin vertical walls. The cells are often columnar and hexagonal in shape. A honeycomb shaped structure provides a material with minimal density and relative high out-of-plane compression properties and out-of-plane shear properties.

Methods have been devised to modify the yield strength, ductility, and toughness of both crystalline and amorphous materials. These strengthening mechanisms give engineers the ability to tailor the mechanical properties of materials to suit a variety of different applications. For example, the favorable properties of steel result from interstitial incorporation of carbon into the iron lattice. Brass, a binary alloy of copper and zinc, has superior mechanical properties compared to its constituent metals due to solution strengthening. Work hardening has also been used for centuries by blacksmiths to introduce dislocations into materials, increasing their yield strengths.

<span class="mw-page-title-main">Colloidal crystal</span> Ordered array of colloidal particles

A colloidal crystal is an ordered array of colloidal particles and fine grained materials analogous to a standard crystal whose repeating subunits are atoms or molecules. A natural example of this phenomenon can be found in the gem opal, where spheres of silica assume a close-packed locally periodic structure under moderate compression. Bulk properties of a colloidal crystal depend on composition, particle size, packing arrangement, and degree of regularity. Applications include photonics, materials processing, and the study of self-assembly and phase transitions.

<span class="mw-page-title-main">Acoustic metamaterial</span> Material designed to manipulate sound waves

An acoustic metamaterial, sonic crystal, or phononic crystal is a material designed to control, direct, and manipulate sound waves or phonons in gases, liquids, and solids. Sound wave control is accomplished through manipulating parameters such as the bulk modulus β, density ρ, and chirality. They can be engineered to either transmit, or trap and amplify sound waves at certain frequencies. In the latter case, the material is an acoustic resonator.

Ultralight materials are solids with a density of less than 10 mg/cm3, including silica aerogels, carbon nanotube aerogels, aerographite, metallic foams, polymeric foams, and metallic microlattices. The density of air is about 1.275 mg/cm3, which means that the air in the pores contributes significantly to the density of these materials in atmospheric conditions. They can be classified by production method as aerogels, stochastic foams, and structured cellular materials.

<span class="mw-page-title-main">Metallic microlattice</span>

A metallic microlattice is a synthetic porous metallic material consisting of an ultra-light metal foam. With a density as low as 0.99 mg/cm3 (0.00561 lb/ft3), it is one of the lightest structural materials known to science. It was developed by a team of scientists from California-based HRL Laboratories, in collaboration with researchers at University of California, Irvine and Caltech, and was first announced in November 2011. The prototype samples were made from a nickel-phosphorus alloy. In 2012, the microlattice prototype was declared one of 10 World-Changing Innovations by Popular Mechanics. Metallic microlattice technology has numerous potential applications in automotive and aeronautical engineering. A detailed comparative review study among other types of metallic lattice structures showed them to be beneficial for light-weighting purposes but expensive to manufacture.

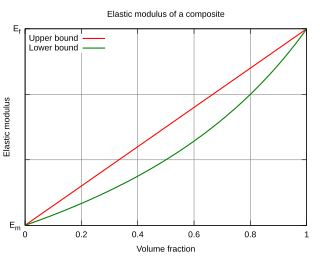
<span class="mw-page-title-main">Rule of mixtures</span>

In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material. It provides a theoretical upper- and lower-bound on properties such as the elastic modulus, ultimate tensile strength, thermal conductivity, and electrical conductivity. In general there are two models, one for axial loading, and one for transverse loading.

Aerographene or graphene aerogel is the least dense solid known to exist, at 160 g/m3. The material reportedly can be produced at the scale of cubic meters.

Tube-based nanostructures are nanolattices made of connected tubes and exhibit nanoscale organization above the molecular level.

The volume (W) and displacement (Δ) indicators have been discovered by Philippe Samyn in 1997 to help the search for the optimal geometry of architectural structures.

Microscale structural metamaterials are synthetic structures that are aimed to yield specific desired mechanical advantages. These designs are often inspired by natural cellular materials such as plant and bone tissue which have superior mechanical efficiency due to their low weight to stiffness ratios.

References

  1. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Cheung, K. C.; Gershenfeld, N. (2013). "Reversibly Assembled Cellular Composite Materials". Science. 341 (6151): 1219–1221. Bibcode:2013Sci...341.1219C. CiteSeerX   10.1.1.672.1351 . doi:10.1126/science.1240889. PMID   23950496. S2CID   206550070.
  2. 1 2 Cheung, K. C.; Gershenfeld, N. (2013-07-17). "Assembling big structures out of small ultralight pieces". Science. 341 (6151): 1219–1221. CiteSeerX   10.1.1.672.1351 . doi:10.1126/science.1240889. PMID   23950496. S2CID   206550070 . Retrieved 2013-08-20.
  3. 1 2 3 4 Cheung, KC; Gershenfeld, N (2013-08-15). "Reversibly Assembled Cellular Composite Materials — Supplementary Materials". Science. 341 (6151): 1219–1221. CiteSeerX   10.1.1.672.1351 . doi:10.1126/science.1240889. PMID   23950496. S2CID   206550070 . Retrieved 2013-08-20.
  4. ↑ ANSYS software
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.