Related Research Articles

In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.
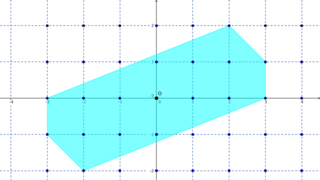
In mathematics, Minkowski's theorem is the statement that every convex set in which is symmetric with respect to the origin and which has volume greater than contains a non-zero integer point. The theorem was proved by Hermann Minkowski in 1889 and became the foundation of the branch of number theory called the geometry of numbers. It can be extended from the integers to any lattice and to any symmetric convex set with volume greater than , where denotes the covolume of the lattice.

Hermann Minkowski was a mathematician and professor at Königsberg, Zürich and Göttingen, described variously as German, Polish, or Lithuanian-German, or Russian. He created and developed the geometry of numbers and elements of convex geometry, and used geometrical methods to solve problems in number theory, mathematical physics, and the theory of relativity.

Geometry of numbers is the part of number theory which uses geometry for the study of algebraic numbers. Typically, a ring of algebraic integers is viewed as a lattice in and the study of these lattices provides fundamental information on algebraic numbers. The geometry of numbers was initiated by Hermann Minkowski.

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B:
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc.

Moritz Werner Fenchel was a German-born Danish mathematician known for his contributions to geometry and to optimization theory. Fenchel established the basic results of convex analysis and nonlinear optimization theory which would, in time, serve as the foundation for nonlinear programming. A German-born Jew and early refugee from Nazi suppression of intellectuals, Fenchel lived most of his life in Denmark. Fenchel's monographs and lecture notes are considered influential.
In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).
In mathematics, Shephard's problem, is the following geometrical question asked by Geoffrey Colin Shephard in 1964: if K and L are centrally symmetric convex bodies in n-dimensional Euclidean space such that whenever K and L are projected onto a hyperplane, the volume of the projection of K is smaller than the volume of the projection of L, then does it follow that the volume of K is smaller than that of L?
In mathematics, particularly, in asymptotic convex geometry, Milman's reverse Brunn–Minkowski inequality is a result due to Vitali Milman that provides a reverse inequality to the famous Brunn–Minkowski inequality for convex bodies in n-dimensional Euclidean space Rn. Namely, it bounds the volume of the Minkowski sum of two bodies from above in terms of the volumes of the bodies.
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.
In differential geometry, the Minkowski problem, named after Hermann Minkowski, asks for the construction of a strictly convex compact surface S whose Gaussian curvature is specified. More precisely, the input to the problem is a strictly positive real function ƒ defined on a sphere, and the surface that is to be constructed should have Gaussian curvature ƒ(n(x)) at the point x, where n(x) denotes the normal to S at x. Eugenio Calabi stated: "From the geometric view point it [the Minkowski problem] is the Rosetta Stone, from which several related problems can be solved."

The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
In convex geometry, the projection body of a convex body in n-dimensional Euclidean space is the convex body such that for any vector , the support function of in the direction u is the (n – 1)-dimensional volume of the projection of K onto the hyperplane orthogonal to u.
Hans Vilhem Rådström (1919–1970) was a Swedish mathematician who worked on complex analysis, continuous groups, convex sets, set-valued analysis, and game theory. From 1952, he was lektor at Stockholm University, and from 1969, he was Professor of Applied Mathematics at Linköping University.
Peter McMullen is a British mathematician, a professor emeritus of mathematics at University College London.
Erwin Lutwak, is a mathematician. Lutwak is professor emeritus at the Courant Institute of Mathematical Sciences at New York University in New York City. His main research interests are convex geometry and its connections with analysis and information theory.
Ruth Silverman was an American mathematician and computer scientist known for her research in computational geometry. She was one of the original founders of the Association for Women in Mathematics in 1971.
In convex geometry and the geometry of convex polytopes, the Blaschke sum of two polytopes is a polytope that has a facet parallel to each facet of the two given polytopes, with the same measure. When both polytopes have parallel facets, the measure of the corresponding facet in the Blaschke sum is the sum of the measures from the two given polytopes.
References
- ↑ Lebens- und Karrieredaten Kürschner Gelehrtenkalender 2009
- ↑ "American Mathematical Society". Ams.org. Retrieved 25 March 2018.
- ↑ https://www.uni-salzburg.at/index.php?id=41747&newsid=3569&s=1ef>
- ↑ Schneider, Rolf (1967). "Zu einem Problem von Shephard über die Projektionen konvexer Körper". Math. Z. (in German). 101: 71–82. doi:10.1007/BF01135693. S2CID 120282582.
- ↑ Schneider, Rolf; Weil, Wolfgang (1992). Integralgeometrie. Teubner. ISBN 3-519-02734-8.
- ↑ Schneider, Rolf; Weil, Wolfgang (2000). Stochastische Geometrie. Stuttgart: Teubner. ISBN 3-519-02740-2.
- ↑ Schneider, Rolf; Weil, Wolfgang (2008). Stochastic and Integral Geometry. Berlin: Springer. ISBN 978-3-540-78858-4.
- ↑ Schneider, Rolf (1993). Convex Bodies: the Brunn-Minkowski Theory . Cambridge University Press. ISBN 0-521-35220-7.
- ↑ Schneider, Rolf (2014). Convex Bodies: the Brunn-Minkowski Theory. Second expanded Edition. Cambridge University Press. ISBN 978-1-107-60101-7.