 | A request that this article title be changed to SOS (paper-and-pencil game) is under discussion . Please do not move this article until the discussion is closed. |
SOS is paper and pencil game for two or more players. It is similar to tic-tac-toe and dots and boxes, but has greater complexity. [1]
SOS is a combinatorial game when played with two players. In terms of game theory, it is a zero-sum, sequential game with perfect information.
Before play begins, a square grid of at least 3×3 squares in size is drawn. Players take turns to add either an "S" or an "O" to any square, with no requirement to use the same letter each turn. The object of the game is for each player to attempt to create the straight sequence S-O-S among connected squares (either diagonally, horizontally, or vertically), and to create as many such sequences as they can. If a player succeeds in creating an SOS, that player immediately takes another turn, and continues to do so until no SOS can be created on their turn. Otherwise turns alternate between players after each move. [2] [3]
Keeping track of who made which SOSs can be done by, e.g., one player circling their SOSs and the other player drawing a line through theirs. Once the grid has been filled up, the winner is the player who made the most SOSs. [3] [4] [5] If the grid is filled up and the number of SOSs for each player is the same, then the game is a draw.
The game can also be played where the player who creates an SOS is the winner and if no SOSs are created the game is a draw. [6]
Dots and boxes is a pencil-and-paper game for two players. It was first published in the 19th century by French mathematician Édouard Lucas, who called it la pipopipette. It has gone by many other names, including the dots and dashes, game of dots, dot to dot grid, boxes, and pigs in a pen.
Tic-tac-toe, noughts and crosses, or Xs and Os is a paper-and-pencil game for two players who take turns marking the spaces in a three-by-three grid with X or O. The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row is the winner. It is a solved game, with a forced draw assuming best play from both players.
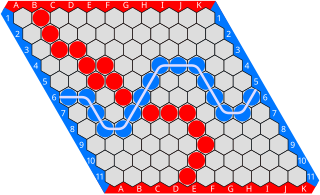
Hex is a two player abstract strategy board game in which players attempt to connect opposite sides of a rhombus-shaped board made of hexagonal cells. Hex was invented by mathematician and poet Piet Hein in 1942 and later rediscovered and popularized by John Nash.
Racetrack is a paper and pencil game that simulates a car race, played by two or more players. The game is played on a squared sheet of paper, with a pencil line tracking each car's movement. The rules for moving represent a car with a certain inertia and physical limits on traction, and the resulting line is reminiscent of how real racing cars move. The game requires players to slow down before bends in the track, and requires some foresight and planning for successful play. The game is popular as an educational tool teaching vectors.
TwixT is a two-player strategy board game, an early entrant in the 1960s 3M bookshelf game series. It became one of the most popular and enduring games in the series. It is a connection game where players alternate turns placing pegs and links on a pegboard in an attempt to link their opposite sides. While TwixT itself is simple, the game also requires strategy, so young children can play it, but it also appeals to adults. The game has been discontinued except in Germany and Japan.
Battleship is a strategy type guessing game for two players. It is played on ruled grids on which each player's fleet of warships are marked. The locations of the fleets are concealed from the other player. Players alternate turns calling "shots" at the other player's ships, and the objective of the game is to destroy the opposing player's fleet.
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.
The Shannon switching game is a connection game for two players, invented by American mathematician and electrical engineer Claude Shannon, the "father of information theory" some time before 1951. Two players take turns coloring the edges of an arbitrary graph. One player has the goal of connecting two distinguished vertices by a path of edges of their color. The other player aims to prevent this by using their color instead. The game is commonly played on a rectangular grid; this special case of the game was independently invented by American mathematician David Gale in the late 1950s and is known as Gale or Bridg-It.
In mathematics, the Hales–Jewett theorem is a fundamental combinatorial result of Ramsey theory named after Alfred W. Hales and Robert I. Jewett, concerning the degree to which high-dimensional objects must necessarily exhibit some combinatorial structure; it is impossible for such objects to be "completely random".
In combinatorial game theory, the strategy-stealing argument is a general argument that shows, for many two-player games, that the second player cannot have a guaranteed winning strategy. The strategy-stealing argument applies to any symmetric game in which an extra move can never be a disadvantage. A key property of a strategy-stealing argument is that it proves that the first player can win the game without actually constructing such a strategy. So, although it might prove the existence of a winning strategy, the proof gives no information about what that strategy is.
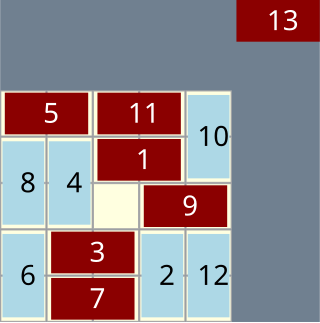
Domineering is a mathematical game that can be played on any collection of squares on a sheet of graph paper. For example, it can be played on a 6×6 square, a rectangle, an entirely irregular polyomino, or a combination of any number of such components. Two players have a collection of dominoes which they place on the grid in turn, covering up squares. One player places tiles vertically, while the other places them horizontally. As in most games in combinatorial game theory, the first player who cannot move loses.
Hackenbush is a two-player game invented by mathematician John Horton Conway. It may be played on any configuration of colored line segments connected to one another by their endpoints and to a "ground" line.
In game theory, a sequential game is a game where one player chooses their action before the others choose theirs. The other players must have information on the first player's choice so that the difference in time has no strategic effect. Sequential games are governed by the time axis and represented in the form of decision trees.
Scrabble variants are games created by changing the normal Scrabble rules or equipment.
Kōnane is a two-player strategy board game from Hawaii. It was invented by the ancient Hawaiian Polynesians. The game is played on a rectangular board. It begins with black and white counters filling the board in an alternating pattern. Players then hop over one another's pieces, capturing them similar to checkers. The first player unable to capture is the loser; their opponent is the winner.
A connection game is a type of abstract strategy game in which players attempt to complete a specific type of connection with their pieces. This could involve forming a path between two or more endpoints, completing a closed loop, or connecting all of one's pieces so they are adjacent to each other. Connection games typically have simple rules, but complex strategies. They have minimal components and may be played as board games, computer games, or even paper-and-pencil games.
The combinatorial game Toads and Frogs is a partisan game invented by Richard Guy. This mathematical game was used as an introductory game in the book Winning Ways for your Mathematical Plays.
Tic-tac-toe is an instance of an m,n,k-game, where two players alternate taking turns on an m×n board until one of them gets k in a row. Harary's generalized tic-tac-toe is an even broader generalization. The game can also be generalized as a nd game. The game can be generalised even further from the above variants by playing on an arbitrary hypergraph where rows are hyperedges and cells are vertices.
Combinatorial Games: Tic-Tac-Toe Theory is a monograph on the mathematics of tic-tac-toe and other positional games, written by József Beck. It was published in 2008 by the Cambridge University Press as volume 114 of their Encyclopedia of Mathematics and its Applications book series (ISBN 978-0-521-46100-9).
In combinatorial game theory, a subtraction game is an abstract strategy game whose state can be represented by a natural number or vector of numbers and in which the allowed moves reduce these numbers. Often, the moves of the game allow any number to be reduced by subtracting a value from a specified subtraction set, and different subtraction games vary in their subtraction sets. These games also vary in whether the last player to move wins or loses. Another winning convention that has also been used is that a player who moves to a position with all numbers zero wins, but that any other position with no moves possible is a draw.
| Variants |  | |
|---|---|---|
| Related concepts | ||
| Similar games | ||