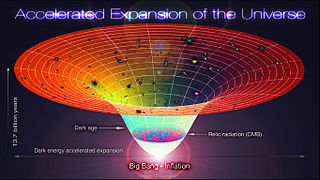
Observations show that the expansion of the universe is accelerating, such that the velocity at which a distant galaxy recedes from the observer is continuously increasing with time. The accelerated expansion of the universe was discovered in 1998 by two independent projects, the Supernova Cosmology Project and the High-Z Supernova Search Team, which used distant type Ia supernovae to measure the acceleration. The idea was that as type Ia supernovae have almost the same intrinsic brightness, and since objects that are farther away appear dimmer, the observed brightness of these supernovae can be used to measure the distance to them. The distance can then be compared to the supernovae's cosmological redshift, which measures how much the universe has expanded since the supernova occurred; the Hubble law established that the farther away that an object is, the faster it is receding. The unexpected result was that objects in the universe are moving away from one another at an accelerating rate. Cosmologists at the time expected that recession velocity would always be decelerating, due to the gravitational attraction of the matter in the universe. Three members of these two groups have subsequently been awarded Nobel Prizes for their discovery. Confirmatory evidence has been found in baryon acoustic oscillations, and in analyses of the clustering of galaxies.
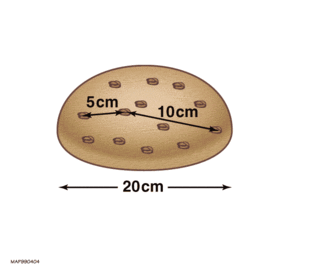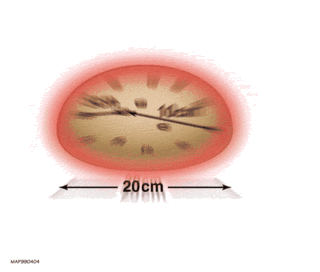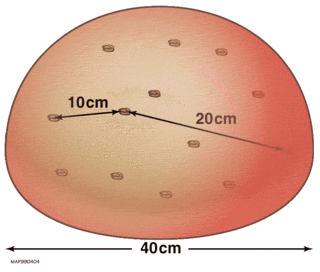
Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving away from Earth. The velocity of the galaxies has been determined by their redshift, a shift of the light they emit toward the red end of the visible spectrum.
In standard cosmology, comoving distance and proper distance are two closely related distance measures used by cosmologists to define distances between objects. Comoving distance factors out the expansion of the universe, giving a distance that does not change in time due to the expansion of space. Proper distance roughly corresponds to where a distant object would be at a specific moment of cosmological time, which can change over time due to the expansion of the universe. Comoving distance and proper distance are defined to be equal at the present time. At other times, the Universe's expansion results in the proper distance changing, while the comoving distance remains constant.
A de Sitter universe is a cosmological solution to the Einstein field equations of general relativity, named after Willem de Sitter. It models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominated by the cosmological constant, thought to correspond to dark energy in our universe or the inflaton field in the early universe. According to the models of inflation and current observations of the accelerating universe, the concordance models of physical cosmology are converging on a consistent model where our universe was best described as a de Sitter universe at about a time seconds after the fiducial Big Bang singularity, and far into the future.
The Friedmann–Lemaître–Robertson–Walker metric is a metric based on the exact solution of the Einstein field equations of general relativity. The metric describes a homogeneous, isotropic, expanding universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are variously grouped as Friedmann, Friedmann–Robertson–Walker (FRW), Robertson–Walker (RW), or Friedmann–Lemaître (FL). This model is sometimes called the Standard Model of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. The FLRW model was developed independently by the named authors in the 1920s and 1930s.
In physical cosmology, the age of the universe is the time elapsed since the Big Bang. Astronomers have derived two different measurements of the age of the universe: a measurement based on direct observations of an early state of the universe, which indicate an age of 13.787±0.020 billion years as interpreted with the Lambda-CDM concordance model as of 2021; and a measurement based on the observations of the local, modern universe, which suggest a younger age. The uncertainty of the first kind of measurement has been narrowed down to 20 million years, based on a number of studies that all show similar figures for the age. These studies include researches of the microwave background radiation by the Planck spacecraft, the Wilkinson Microwave Anisotropy Probe and other space probes. Measurements of the cosmic background radiation give the cooling time of the universe since the Big Bang, and measurements of the expansion rate of the universe can be used to calculate its approximate age by extrapolating backwards in time. The range of the estimate is also within the range of the estimate for the oldest observed star in the universe.
The Lambda-CDM, Lambda cold dark matter or ΛCDM model is a mathematical model of the Big Bang theory with three major components:
- a cosmological constant denoted by lambda (Λ) associated with dark energy,
- the postulated cold dark matter, and
- ordinary matter.
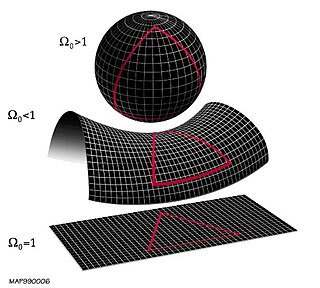
The flatness problem is a cosmological fine-tuning problem within the Big Bang model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that small deviations from these values would have extreme effects on the appearance of the universe at the current time.

The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density ρ and pressure p. The equations for negative spatial curvature were given by Friedmann in 1924.
In cosmology, the equation of state of a perfect fluid is characterized by a dimensionless number , equal to the ratio of its pressure to its energy density :
In physical cosmology, structure formation is the formation of galaxies, galaxy clusters and larger structures from small early density fluctuations. The universe, as is now known from observations of the cosmic microwave background radiation, began in a hot, dense, nearly uniform state approximately 13.8 billion years ago. However, looking at the night sky today, structures on all scales can be seen, from stars and planets to galaxies. On even larger scales, galaxy clusters and sheet-like structures of galaxies are separated by enormous voids containing few galaxies. Structure formation attempts to model how these structures were formed by gravitational instability of small early ripples in spacetime density or another emergence.
In cosmology, a static universe is a cosmological model in which the universe is both spatially and temporally infinite, and space is neither expanding nor contracting. Such a universe does not have so-called spatial curvature; that is to say that it is 'flat' or Euclidean. A static infinite universe was first proposed by English astronomer Thomas Digges (1546–1595).
The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion; the universe does not expand "into" anything and does not require space to exist "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation only applies with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.
The deceleration parameter in cosmology is a dimensionless measure of the cosmic acceleration of the expansion of space in a Friedmann–Lemaître–Robertson–Walker universe. It is defined by:
Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly observable, but is more convenient for calculations. The distance measures discussed here all reduce to the common notion of Euclidean distance at low redshift.
In physical cosmology and astronomy, dark energy is an unknown form of energy that affects the universe on the largest scales. Its primary effect is to drive the accelerating expansion of the universe. Assuming that the lambda-CDM model of cosmology is correct, dark energy is the dominant component of the universe, contributing 68% of the total energy in the present-day observable universe while dark matter and ordinary (baryonic) matter contribute 26% and 5%, respectively, and other components such as neutrinos and photons are nearly negligible. Dark energy's density is very low: 6×10−10 J/m3, much less than the density of ordinary matter or dark matter within galaxies. However, it dominates the universe's mass–energy content because it is uniform across space.
In cosmology, baryon acoustic oscillations (BAO) are fluctuations in the density of the visible baryonic matter of the universe, caused by acoustic density waves in the primordial plasma of the early universe. In the same way that supernovae provide a "standard candle" for astronomical observations, BAO matter clustering provides a "standard ruler" for length scale in cosmology. The length of this standard ruler is given by the maximum distance the acoustic waves could travel in the primordial plasma before the plasma cooled to the point where it became neutral atoms, which stopped the expansion of the plasma density waves, "freezing" them into place. The length of this standard ruler can be measured by looking at the large scale structure of matter using astronomical surveys. BAO measurements help cosmologists understand more about the nature of dark energy by constraining cosmological parameters.
The Einstein–de Sitter universe is a model of the universe proposed by Albert Einstein and Willem de Sitter in 1932. On first learning of Edwin Hubble's discovery of a linear relation between the redshift of the galaxies and their distance, Einstein set the cosmological constant to zero in the Friedmann equations, resulting in a model of the expanding universe known as the Friedmann–Einstein universe. In 1932, Einstein and De Sitter proposed an even simpler cosmic model by assuming a vanishing spatial curvature as well as a vanishing cosmological constant. In modern parlance, the Einstein–de Sitter universe can be described as a cosmological model for a flat matter-only Friedmann–Lemaître–Robertson–Walker metric (FLRW) universe.
Mattig's formula was an important formula in observational cosmology and extragalactic astronomy which gives relation between radial coordinate and redshift of a given source. It depends on the cosmological model being used and is used to calculate luminosity distance in terms of redshift.
The cosmic age problem was a historical problem in astronomy concerning the age of the universe. The problem was that at various times in the 20th century, the universe was estimated to be younger than the oldest observed stars. Estimates of the universe's age came from measurements of the current expansion rate of the universe, the Hubble constant , as well as cosmological models relating to the universe's matter and energy contents. Issues with measuring as well as not knowing about the existence of dark energy led to spurious estimates of the age. Additionally, objects such as galaxies, stars, and planets could not have existed in the extreme temperatures and densities shortly after the Big Bang.































