In mathematics, the Schreier refinement theorem of group theory states that any two subnormal series of subgroups of a given group have equivalent refinements, where two series are equivalent if there is a bijection between their factor groups that sends each factor group to an isomorphic one.
The theorem is named after the Austrian mathematician Otto Schreier who proved it in 1928. It provides an elegant proof of the Jordan–Hölder theorem. It is often proved using the Zassenhaus lemma. Baumslag (2006) gives a short proof by intersecting the terms in one subnormal series with those in the other series.
Consider , where is the symmetric group of degree 3. The alternating group is a normal subgroup of , so we have the two subnormal series
with respective factor groups and .
The two subnormal series are not equivalent, but they have equivalent refinements:
with factor groups isomorphic to and
with factor groups isomorphic to .
In the mathematical field of group theory, Lagrange's theorem is a theorem that states that for any finite group G, the order of every subgroup of G divides the order of G. The theorem is named after Joseph-Louis Lagrange. The following variant states that for a subgroup of a finite group , not only is an integer, but its value is the index , defined as the number of left cosets of in .
In mathematics, specifically abstract algebra, the isomorphism theorems are theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures. In universal algebra, the isomorphism theorems can be generalized to the context of algebras and congruences.
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, namely a nontrivial normal subgroup and the corresponding quotient group. This process can be repeated, and for finite groups one eventually arrives at uniquely determined simple groups, by the Jordan–Hölder theorem.
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements in such that every in can be written in the form for some integers . In this case, we say that the set is a generating set of or that generate.
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates in the trivial subgroup.
In mathematics, specifically group theory, a nilpotent groupG is a group that has an upper central series that terminates with G. Equivalently, it has a central series of finite length or its lower central series terminates with {1}.
In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free-modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.
A group is a set together with an associative operation that admits an identity element and such that there exists an inverse for every element.
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence cannot be decomposed into a direct sum of simple modules. A composition series of a module M is a finite increasing filtration of M by submodules such that the successive quotients are simple and serves as a replacement of the direct sum decomposition of M into its simple constituents.
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If and are two groups, then is an extension of by if there is a short exact sequence
In mathematics, more specifically in group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no non-trivial abelian quotients. In symbols, a perfect group is one such that G(1) = G, or equivalently one such that Gab = {1}.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
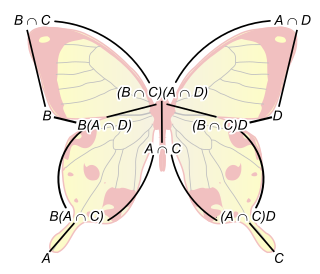
In mathematics, the butterfly lemma or Zassenhaus lemma, named after Hans Zassenhaus, is a technical result on the lattice of subgroups of a group or the lattice of submodules of a module, or more generally for any modular lattice.
In mathematics, specifically group theory, a subgroup series of a group is a chain of subgroups:
In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov. The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.
In mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.
In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of Rn, this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood.
In mathematics, the Krull–Schmidt theorem states that a group subjected to certain finiteness conditions on chains of subgroups, can be uniquely written as a finite direct product of indecomposable subgroups.
In the mathematical subject of group theory, the Howson property, also known as the finitely generated intersection property (FGIP), is the property of a group saying that the intersection of any two finitely generated subgroups of this group is again finitely generated. The property is named after Albert G. Howson who in a 1954 paper established that free groups have this property.
 | This abstract algebra-related article is a stub. You can help Wikipedia by expanding it. |
