Selberg integral

Last updated November 26, 2023

In mathematics, the Selberg integral is a generalization of Euler beta function to n dimensions introduced by Atle Selberg.^[1]^[2]

Selberg's integral formula

When $Re(\alpha )>0,Re(\beta )>0,Re(\gamma )>-\min \left({\frac {1}{n}},{\frac {Re(\alpha )}{n-1}},{\frac {Re(\beta )}{n-1}}\right)$ , we have

{\begin{aligned}S_{n}(\alpha ,\beta ,\gamma )&=\int _{0}^{1}\cdots \int _{0}^{1}\prod _{i=1}^{n}t_{i}^{\alpha -1}(1-t_{i})^{\beta -1}\prod _{1\leq i<j\leq n}|t_{i}-t_{j}|^{2\gamma }\,dt_{1}\cdots dt_{n}\\&=\prod _{j=0}^{n-1}{\frac {\Gamma (\alpha +j\gamma )\Gamma (\beta +j\gamma )\Gamma (1+(j+1)\gamma )}{\Gamma (\alpha +\beta +(n+j-1)\gamma )\Gamma (1+\gamma )}}\end{aligned}}

Selberg's formula implies Dixon's identity for well poised hypergeometric series, and some special cases of Dyson's conjecture. This is a corollary of Aomoto.

Aomoto's integral formula

Aomoto proved a slightly more general integral formula.^[3] With the same conditions as Selberg's formula,

\int _{0}^{1}\cdots \int _{0}^{1}\left(\prod _{i=1}^{k}t_{i}\right)\prod _{i=1}^{n}t_{i}^{\alpha -1}(1-t_{i})^{\beta -1}\prod _{1\leq i<j\leq n}|t_{i}-t_{j}|^{2\gamma }\,dt_{1}\cdots dt_{n}

=S_{n}(\alpha ,\beta ,\gamma )\prod _{j=1}^{k}{\frac {\alpha +(n-j)\gamma }{\alpha +\beta +(2n-j-1)\gamma }}.

A proof is found in Chapter 8 of Andrews, Askey & Roy (1999).^[4]

Mehta's integral

When $Re(\gamma )>-1/n$ ,

{\frac {1}{(2\pi )^{n/2}}}\int _{-\infty }^{\infty }\cdots \int _{-\infty }^{\infty }\prod _{i=1}^{n}e^{-t_{i}^{2}/2}\prod _{1\leq i<j\leq n}|t_{i}-t_{j}|^{2\gamma }\,dt_{1}\cdots dt_{n}=\prod _{j=1}^{n}{\frac {\Gamma (1+j\gamma )}{\Gamma (1+\gamma )}}.

It is a corollary of Selberg, by setting $\alpha =\beta$ , and change of variables with $t_{i}={\frac {1+t'_{i}/{\sqrt {2\alpha }}}{2}}$ , then taking $\alpha \to \infty$ .

This was conjectured by Mehta & Dyson (1963), who were unaware of Selberg's earlier work.^[5]

It is the partition function for a gas of point charges moving on a line that are attracted to the origin.^[6]

Macdonald's integral

Macdonald (1982) conjectured the following extension of Mehta's integral to all finite root systems, Mehta's original case corresponding to the A_n−1 root system.^[7]

{\frac {1}{(2\pi )^{n/2}}}\int \cdots \int \left|\prod _{r}{\frac {2(x,r)}{(r,r)}}\right|^{\gamma }e^{-(x_{1}^{2}+\cdots +x_{n}^{2})/2}dx_{1}\cdots dx_{n}=\prod _{j=1}^{n}{\frac {\Gamma (1+d_{j}\gamma )}{\Gamma (1+\gamma )}}

The product is over the roots r of the roots system and the numbers d_j are the degrees of the generators of the ring of invariants of the reflection group. Opdam (1989) gave a uniform proof for all crystallographic reflection groups.^[8] Several years later he proved it in full generality, making use of computer-aided calculations by Garvan.^[9]

Related Research Articles

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer $n$ ,

<span class="mw-page-title-main">Taylor's theorem</span> Approximation of a function by a truncated power series

In calculus, Taylor's theorem gives an approximation of a $-times differentiable function around a given point by a polynomial of degree, called the -th-order Taylor polynomial . For a smooth function, the Taylor polynomial is the truncation at the order of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation . There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.$

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

In quantum field theory, the Lehmann–Symanzik–Zimmermann (LSZ) reduction formula is a method to calculate S-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann.

In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.

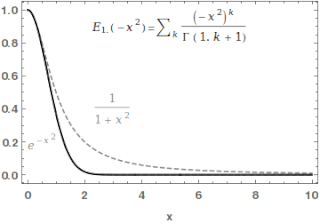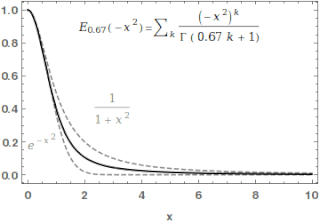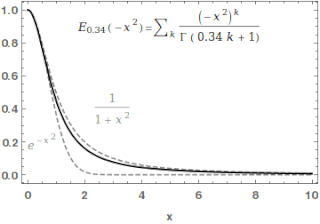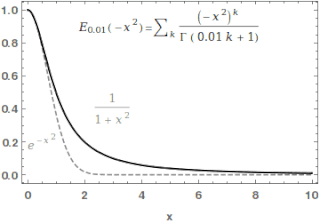
In mathematics, the Mittag-Leffler function $is a special function, a complex function which depends on two complex parameters and . It may be defined by the following series when the real part of is strictly positive:$

In mathematics, the Nørlund–Rice integral, sometimes called Rice's method, relates the nth forward difference of a function to a line integral on the complex plane. It commonly appears in the theory of finite differences and has also been applied in computer science and graph theory to estimate binary tree lengths. It is named in honour of Niels Erik Nørlund and Stephen O. Rice. Nørlund's contribution was to define the integral; Rice's contribution was to demonstrate its utility by applying saddle-point techniques to its evaluation.

In natural language processing, latent Dirichlet allocation (LDA) is a Bayesian network that explains a set of observations through unobserved groups, and each group explains why some parts of the data are similar. The LDA is an example of a Bayesian topic model. In this, observations are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics.

Continuous wavelets of compact support alpha can be built, which are related to the beta distribution. The process is derived from probability distributions using blur derivative. These new wavelets have just one cycle, so they are termed unicycle wavelets. They can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two parameters $and . Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko and Kolmogorov applied for compactly supported signals.$

A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is

In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

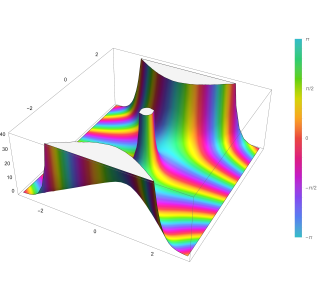
In mathematics, the Fox H-functionH(x) is a generalization of the Meijer G-function and the Fox–Wright function introduced by Charles Fox (1961). It is defined by a Mellin–Barnes integral

A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product $is a product distribution .$

In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.

In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the derivative dealing with the measurement of fractals, defined in fractal geometry. Fractal derivatives were created for the study of anomalous diffusion, by which traditional approaches fail to factor in the fractal nature of the media. A fractal measure t is scaled according to t^α. Such a derivative is local, in contrast to the similarly applied fractional derivative. Fractal calculus is formulated as a generalized of standard calculus

In mathematics, Katugampola fractional operators are integral operators that generalize the Riemann–Liouville and the Hadamard fractional operators into a unique form. The Katugampola fractional integral generalizes both the Riemann–Liouville fractional integral and the Hadamard fractional integral into a single form and It is also closely related to the Erdelyi–Kober operator that generalizes the Riemann–Liouville fractional integral. Katugampola fractional derivative has been defined using the Katugampola fractional integral and as with any other fractional differential operator, it also extends the possibility of taking real number powers or complex number powers of the integral and differential operators.

In mathematics, the Faxén integral is the following integral

References

↑ Selberg, Atle (1944). "Remarks on a multiple integral" . Norsk Mat. Tidsskr. 26: 71–78. MR 0018287.
↑ Forrester, Peter J.; Warnaar, S. Ole (2008). "The importance of the Selberg integral". Bull. Amer. Math. Soc. 45 (4): 489–534. arXiv: 0710.3981 . doi:10.1090/S0273-0979-08-01221-4. S2CID 14185100.
↑ Aomoto, K (1987). "On the complex Selberg integral" . The Quarterly Journal of Mathematics. 38 (4): 385–399. doi:10.1093/qmath/38.4.385.
↑ Andrews, George; Askey, Richard; Roy, Ranjan (1999). "The Selberg integral and its applications". Special functions. Encyclopedia of Mathematics and its Applications. Vol. 71. Cambridge University Press. ISBN 978-0-521-62321-6. MR 1688958.
↑ Mehta, Madan Lal; Dyson, Freeman J. (1963). "Statistical theory of the energy levels of complex systems. V" . Journal of Mathematical Physics . 4 (5): 713–719. Bibcode:1963JMP.....4..713M. doi:10.1063/1.1704009. MR 0151232.
↑ Mehta, Madan Lal (2004). Random matrices. Pure and Applied Mathematics (Amsterdam). Vol. 142 (3rd ed.). Elsevier/Academic Press, Amsterdam. ISBN 978-0-12-088409-4. MR 2129906.
↑ Macdonald, I. G. (1982). "Some conjectures for root systems". SIAM Journal on Mathematical Analysis. 13 (6): 988–1007. doi:10.1137/0513070. ISSN 0036-1410. MR 0674768.
↑ Opdam, E.M. (1989). "Some applications of hypergeometric shift operators". Invent. Math. 98 (1): 275–282. Bibcode:1989InMat..98....1O. doi:10.1007/BF01388841. MR 1010152. S2CID 54571505.
↑ Opdam, E.M. (1993). "Dunkl operators, Bessel functions and the discriminant of a finite Coxeter group". Compositio Mathematica. 85 (3): 333–373. MR 1214452. Zbl 0778.33009.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Selberg, Atle (1944). "Remarks on a multiple integral" . Norsk Mat. Tidsskr. 26: 71–78. MR 0018287.

[2] Forrester, Peter J.; Warnaar, S. Ole (2008). "The importance of the Selberg integral". Bull. Amer. Math. Soc. 45 (4): 489–534. arXiv: 0710.3981 . doi:10.1090/S0273-0979-08-01221-4. S2CID 14185100.

[3] Aomoto, K (1987). "On the complex Selberg integral" . The Quarterly Journal of Mathematics. 38 (4): 385–399. doi:10.1093/qmath/38.4.385.

[4] Andrews, George; Askey, Richard; Roy, Ranjan (1999). "The Selberg integral and its applications". Special functions. Encyclopedia of Mathematics and its Applications. Vol. 71. Cambridge University Press. ISBN 978-0-521-62321-6. MR 1688958.

[5] Mehta, Madan Lal; Dyson, Freeman J. (1963). "Statistical theory of the energy levels of complex systems. V" . Journal of Mathematical Physics . 4 (5): 713–719. Bibcode:1963JMP.....4..713M. doi:10.1063/1.1704009. MR 0151232.

[6] Mehta, Madan Lal (2004). Random matrices. Pure and Applied Mathematics (Amsterdam). Vol. 142 (3rd ed.). Elsevier/Academic Press, Amsterdam. ISBN 978-0-12-088409-4. MR 2129906.

[7] Macdonald, I. G. (1982). "Some conjectures for root systems". SIAM Journal on Mathematical Analysis. 13 (6): 988–1007. doi:10.1137/0513070. ISSN 0036-1410. MR 0674768.

[8] Opdam, E.M. (1989). "Some applications of hypergeometric shift operators". Invent. Math. 98 (1): 275–282. Bibcode:1989InMat..98....1O. doi:10.1007/BF01388841. MR 1010152. S2CID 54571505.

[9] Opdam, E.M. (1993). "Dunkl operators, Bessel functions and the discriminant of a finite Coxeter group". Compositio Mathematica. 85 (3): 333–373. MR 1214452. Zbl 0778.33009.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]