Shear thinning

Last updated July 21, 2024

In rheology, shear thinning is the non-Newtonian behavior of fluids whose viscosity decreases under shear strain. It is sometimes considered synonymous for pseudo-plastic behaviour,^[1]^[2] and is usually defined as excluding time-dependent effects, such as thixotropy.^[3]

Shear thinning is the most common type of non-Newtonian behavior of fluids and is seen in many industrial and everyday applications.^[4] Although shear thinning is generally not observed in pure liquids with low molecular mass or ideal solutions of small molecules like sucrose or sodium chloride, it is often observed in polymer solutions and molten polymers, as well as complex fluids and suspensions like ketchup, whipped cream, blood,^[5] paint, and nail polish.

Theories behind shear-thinning behaviour

Though the exact cause of shear thinning is not fully understood, it is widely regarded to be the effect of small structural changes within the fluid, such that microscale geometries within the fluid rearrange to facilitate shearing.^[6] In colloid systems, phase separation during flow leads to shear thinning. In polymer systems such as polymer melts and solutions, shear thinning is caused by the disentanglement of polymer chains during flow. At rest, high molecular weight polymers are entangled and randomly oriented. However, when undergoing agitation at a high enough rate, these highly anisotropic polymer chains start to disentangle and align along the direction of the shear force.^[7] This leads to less molecular/particle interaction and a larger amount of free space, decreasing the viscosity.^[4]

Power law model

At both sufficiently high and very low shear rates, viscosity of a polymer system is independent of the shear rate. At high shear rates, polymers are entirely disentangled and the viscosity value of the system plateaus at η_∞, or the infinite shear viscosity plateau. At low shear rates, the shear is too low to be impeded by entanglements and the viscosity value of the system is η₀, or the zero shear rate viscosity. The value of η_∞ represents the lowest viscosity attainable and may be orders of magnitude lower than η₀, depending on the degree of shear thinning.

Viscosity is plotted against shear rate in a log(η) vs. log( ${\dot {\gamma }}$ ) plot, where the linear region is the shear-thinning regime and can be expressed using the Ostwald and de Waele power law equation:^[8]

\tau =K(T)\left({d\gamma  \over dt}\right)^{n}=K(T){\dot {\gamma }}^{n}

The Ostwald and de Waele equation can be written in a logarithmic form:

\log(\tau )=\log(K)+n\log \left({\dot {\gamma }}\right)

The apparent viscosity is defined as $\eta ={\tau \over {\dot {\gamma }}}$ , and this may be plugged into the Ostwald equation to yield a second power-law equation for apparent viscosity:

\eta =K(T){\dot {\gamma }}^{n-1}

This expression can also be used to describe dilatant (shear thickening) behaviour, where the value of n is greater than 1.

Herschel-Bulkley model

Bingham plastics require a critical shear stress to be exceeded in order to start flowing. This behaviour is usually seen in polymer/silica micro- and nanocomposites, where the formation of a silica network in the material provides a solid-like response at low shear stress. The shear-thinning behavior of plastic fluids can be described with the Herschel-Bulkley model, which adds a threshold shear stress component to the Ostwald equation:^[8]

\tau =\tau _{y}+K(T){\dot {\gamma }}^{n}

Relationship with thixotropy

Some authors consider shear thinning to be a special case of thixotropic behaviour, because the recovery of the microstructure of the liquid to its initial state will always require a non-zero time. When the recovery of viscosity after disturbance is very rapid however, the observed behaviour is classic shear thinning or pseudoplasticity, because as soon as the shear is removed, the viscosity returns to normal. When it takes a measurable time for the viscosity to recover, thixotropic behaviour is observed.^[9] When describing the viscosity of liquids, however, it is therefore useful to distinguish shear-thinning (pseudoplastic) behaviour from thixotropic behaviour, where the viscosity at all shear rates is decreased for some duration after agitation: both of these effects can often be seen separately in the same liquid.^[10]

Everyday examples

Wall paint is a pseudoplastic material.^[11] When modern wall paint is applied, the shear created by the brush or roller will allow it to thin and wet out the surface evenly. Once applied, the paint regains its higher viscosity, which avoids drips and runs.

Ketchup is a shear-thinning material, viscous when at rest, but flowing at speed when agitated by squeezing, shaking, or striking the bottle.^[11]

Whipped cream is also a shear-thinning material.^[6] When whipped cream is sprayed out of its canister, it flows out smoothly from the nozzle due to the low viscosity at high flow rate. However, after whipped cream is sprayed into a spoon, it does not flow and its increased viscosity allows it to be rigid.

External links

The Great Ketchup Mystery

Related Research Articles

Rheology is the study of the flow of matter, primarily in a fluid state but also as "soft solids" or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force. Rheology is the branch of physics that deals with the deformation and flow of materials, both solids and liquids.

A viscometer is an instrument used to measure the viscosity of a fluid. For liquids with viscosities which vary with flow conditions, an instrument called a rheometer is used. Thus, a rheometer can be considered as a special type of viscometer. Viscometers can measure only constant viscosity, that is, viscosity that does not change with flow conditions.

A non-Newtonian fluid is a fluid that does not follow Newton's law of viscosity, that is, it has variable viscosity dependent on stress. In particular, the viscosity of non-Newtonian fluids can change when subjected to force. Ketchup, for example, becomes runnier when shaken and is thus a non-Newtonian fluid. Many salt solutions and molten polymers are non-Newtonian fluids, as are many commonly found substances such as custard, toothpaste, starch suspensions, corn starch, paint, blood, melted butter, and shampoo.

A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

Shear stress is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. Normal stress, on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts.

In continuum mechanics, a power-law fluid, or the Ostwald–de Waele relationship, is a type of generalized Newtonian fluid for which the shear stress, $τ$ , is given by

Hemorheology, also spelled haemorheology, or blood rheology, is the study of flow properties of blood and its elements of plasma and cells. Proper tissue perfusion can occur only when blood's rheological properties are within certain levels. Alterations of these properties play significant roles in disease processes. Blood viscosity is determined by plasma viscosity, hematocrit and mechanical properties of red blood cells. Red blood cells have unique mechanical behavior, which can be discussed under the terms erythrocyte deformability and erythrocyte aggregation. Because of that, blood behaves as a non-Newtonian fluid. As such, the viscosity of blood varies with shear rate. Blood becomes less viscous at high shear rates like those experienced with increased flow such as during exercise or in peak-systole. Therefore, blood is a shear-thinning fluid. Contrarily, blood viscosity increases when shear rate goes down with increased vessel diameters or with low flow, such as downstream from an obstruction or in diastole. Blood viscosity also increases with increases in red cell aggregability.

In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist both shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed.

Thixotropy is a time-dependent shear thinning property. Certain gels or fluids that are thick or viscous under static conditions will flow over time when shaken, agitated, shear-stressed, or otherwise stressed. They then take a fixed time to return to a more viscous state. Some non-Newtonian pseudoplastic fluids show a time-dependent change in viscosity; the longer the fluid undergoes shear stress, the lower its viscosity. A thixotropic fluid is a fluid which takes a finite time to attain equilibrium viscosity when introduced to a steep change in shear rate. Some thixotropic fluids return to a gel state almost instantly, such as ketchup, and are called pseudoplastic fluids. Others such as yogurt take much longer and can become nearly solid. Many gels and colloids are thixotropic materials, exhibiting a stable form at rest but becoming fluid when agitated. Thixotropy arises because particles or structured solutes require time to organize.

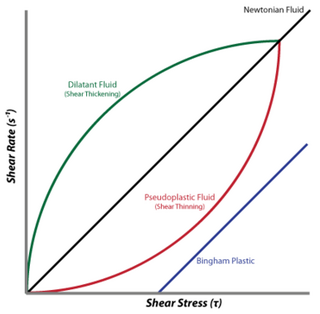
A dilatant material is one in which viscosity increases with the rate of shear strain. Such a shear thickening fluid, also known by the initialism STF, is an example of a non-Newtonian fluid. This behaviour is usually not observed in pure materials, but can occur in suspensions.

A generalized Newtonian fluid is an idealized fluid for which the shear stress is a function of shear rate at the particular time, but not dependent upon the history of deformation. Although this type of fluid is non-Newtonian in nature, its constitutive equation is a generalised form of the Newtonian fluid. Generalised Newtonian fluids satisfy the following rheological equation:

Rheometry generically refers to the experimental techniques used to determine the rheological properties of materials, that is the qualitative and quantitative relationships between stresses and strains and their derivatives. The techniques used are experimental. Rheometry investigates materials in relatively simple flows like steady shear flow, small amplitude oscillatory shear, and extensional flow.

The upper-convected Maxwell (UCM) model is a generalisation of the Maxwell material for the case of large deformations using the upper-convected time derivative. The model was proposed by James G. Oldroyd. The concept is named after James Clerk Maxwell.

In fluid mechanics, apparent viscosity is the shear stress applied to a fluid divided by the shear rate:

The Herschel–Bulkley fluid is a generalized model of a non-Newtonian fluid, in which the strain experienced by the fluid is related to the stress in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress $. The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.$

Rheological weldability (RW) of thermoplastics considers the materials flow characteristics in determining the weldability of the given material. The process of welding thermal plastics requires three general steps, first is surface preparation. The second step is the application of heat and pressure to create intimate contact between the components being joined and initiate inter-molecular diffusion across the joint and the third step is cooling. RW can be used to determine the effectiveness of the second step of the process for given materials.

In continuum mechanics, time-dependent viscosity is a property of fluids whose viscosity changes as a function of time. The most common type of this is thixotropy, in which the viscosity of fluids under continuous shear decreases with time; the opposite is rheopecty, in which viscosity increases with time.

An important class of non-Newtonian fluids presents a yield stress limit which must be exceeded before significant deformation can occur – the so-called viscoplastic fluids or Bingham plastics. In order to model the stress-strain relation in these fluids, some fitting have been proposed such as the linear Bingham equation and the non-linear Herschel-Bulkley and Casson models.

Capillary breakup rheometry is an experimental technique used to assess the extensional rheological response of low viscous fluids. Unlike most shear and extensional rheometers, this technique does not involve active stretch or measurement of stress or strain but exploits only surface tension to create a uniaxial extensional flow. Hence, although it is common practice to use the name rheometer, capillary breakup techniques should be better addressed to as indexers.

Squeeze flow is a type of flow in which a material is pressed out or deformed between two parallel plates or objects. First explored in 1874 by Josef Stefan, squeeze flow describes the outward movement of a droplet of material, its area of contact with the plate surfaces, and the effects of internal and external factors such as temperature, viscoelasticity, and heterogeneity of the material. Several squeeze flow models exist to describe Newtonian and non-Newtonian fluids undergoing squeeze flow under various geometries and conditions. Numerous applications across scientific and engineering disciplines including rheometry, welding engineering, and materials science provide examples of squeeze flow in practical use.

References

↑ Mezger, Thomas G. (2006). The rheology handbook : for users of rotational and oscillatory rheometers (2., rev. ed.). Hannover: Vincentz Network. p. 34. ISBN 9783878701743.
↑ Heldman, R. Paul Singh, Dennis R. (2013). Introduction to food engineering (5th ed.). Amsterdam: Elsevier. p. 160. ISBN 9780124016750.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Bair, Scott (2007). High-pressure rheology for quantitative elastohydrodynamics (1st ed.). Amsterdam: Elsevier. p. 136. ISBN 9780080475301 . Retrieved 24 May 2015.
1 2 Malvern Instruments Worldwide. "A Basic Introduction to Rheology" (PDF). Retrieved 12 December 2019.
↑ Tazraei, P.; Riasi, A.; Takabi, B. (2015). "The influence of the non-Newtonian properties of blood on blood-hammer through the posterior cerebral artery". Mathematical Biosciences. 264: 119–127. doi:10.1016/j.mbs.2015.03.013. PMID 25865933.
1 2 "The Physics of Whipped Cream". NASA Science. 25 April 2008. Retrieved 20 August 2023.
↑ "Viscosity of Newtonian and Non-Newtonian Fluids". Rheosense Inc. Retrieved 12 December 2019.
1 2 "Flow Properties of Polymers". polymerdatabase.com. Retrieved 12 December 2019.
↑ Barnes, Howard A. (1997). "Thixotropy a review" (PDF). J. Non-Newtonian Fluid Mech., 70: 3. Archived from the original (PDF) on 30 April 2016. Retrieved 11 November 2011.
↑ Troy, David B. (2005). Remington : The science and practice of pharmacy (21st ed.). Philadelphia: Lippincott, Williams & Wilkins. p. 344. ISBN 9780781746731 . Retrieved 24 May 2015.
1 2 Schlichting, H. Joachim (12 March 2021). "Ketchup Is Not Just a Condiment: It Is Also a Non-Newtonian Fluid". Scientific American. Retrieved 20 August 2023.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Mezger, Thomas G. (2006). The rheology handbook : for users of rotational and oscillatory rheometers (2., rev. ed.). Hannover: Vincentz Network. p. 34. ISBN 9783878701743.

[2] Heldman, R. Paul Singh, Dennis R. (2013). Introduction to food engineering (5th ed.). Amsterdam: Elsevier. p. 160. ISBN 9780124016750.{{cite book}}: CS1 maint: multiple names: authors list (link)

[3] Bair, Scott (2007). High-pressure rheology for quantitative elastohydrodynamics (1st ed.). Amsterdam: Elsevier. p. 136. ISBN 9780080475301 . Retrieved 24 May 2015.

[:0-4] 1 2 Malvern Instruments Worldwide. "A Basic Introduction to Rheology" (PDF). Retrieved 12 December 2019.

[5] Tazraei, P.; Riasi, A.; Takabi, B. (2015). "The influence of the non-Newtonian properties of blood on blood-hammer through the posterior cerebral artery". Mathematical Biosciences. 264: 119–127. doi:10.1016/j.mbs.2015.03.013. PMID 25865933.

[:3-6] 1 2 "The Physics of Whipped Cream". NASA Science. 25 April 2008. Retrieved 20 August 2023.

[7] "Viscosity of Newtonian and Non-Newtonian Fluids". Rheosense Inc. Retrieved 12 December 2019.

[:1-8] 1 2 "Flow Properties of Polymers". polymerdatabase.com. Retrieved 12 December 2019.

[9] Barnes, Howard A. (1997). "Thixotropy a review" (PDF). J. Non-Newtonian Fluid Mech., 70: 3. Archived from the original (PDF) on 30 April 2016. Retrieved 11 November 2011.

[10] Troy, David B. (2005). Remington : The science and practice of pharmacy (21st ed.). Philadelphia: Lippincott, Williams & Wilkins. p. 344. ISBN 9780781746731 . Retrieved 24 May 2015.

[:2-11] 1 2 Schlichting, H. Joachim (12 March 2021). "Ketchup Is Not Just a Condiment: It Is Also a Non-Newtonian Fluid". Scientific American. Retrieved 20 August 2023.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]