Shelling (topology)

Last updated August 27, 2024

In mathematics, a shelling of a simplicial complex is a way of gluing it together from its maximal simplices (simplices that are not a face of another simplex) in a well-behaved way. A complex admitting a shelling is called shellable.

Definition

A d-dimensional simplicial complex is called pure if its maximal simplices all have dimension d. Let $\Delta$ be a finite or countably infinite simplicial complex. An ordering $C_{1},C_{2},\ldots$ of the maximal simplices of $\Delta$ is a shelling if, for all $k=2,3,\ldots$ , the complex

B_{k}:={\Big (}\bigcup _{i=1}^{k-1}C_{i}{\Big )}\cap C_{k}

is pure and of dimension one smaller than $\dim C_{k}$ . That is, the "new" simplex $C_{k}$ meets the previous simplices along some union $B_{k}$ of top-dimensional simplices of the boundary of $C_{k}$ . If $B_{k}$ is the entire boundary of $C_{k}$ then $C_{k}$ is called spanning.

For $\Delta$ not necessarily countable, one can define a shelling as a well-ordering of the maximal simplices of $\Delta$ having analogous properties.

Properties

A shellable complex is homotopy equivalent to a wedge sum of spheres, one for each spanning simplex of corresponding dimension.
A shellable complex may admit many different shellings, but the number of spanning simplices and their dimensions do not depend on the choice of shelling. This follows from the previous property.

Examples

Every Coxeter complex, and more generally every building (in the sense of Tits), is shellable.^[1]

The boundary complex of a (convex) polytope is shellable.^[2]^[3] Note that here, shellability is generalized to the case of polyhedral complexes (that are not necessarily simplicial).

There is an unshellable triangulation of the tetrahedron.^[4]

Notes

↑ Björner, Anders (1984). "Some combinatorial and algebraic properties of Coxeter complexes and Tits buildings". Advances in Mathematics . 52 (3): 173–212. doi: 10.1016/0001-8708(84)90021-5 . ISSN 0001-8708.
↑ Bruggesser, H.; Mani, P. "Shellable Decompositions of Cells and Spheres". Mathematica Scandinavica. 29: 197–205. doi: 10.7146/math.scand.a-11045 .
↑ Ziegler, Günter M. "8.2. Shelling polytopes". Lectures on polytopes. Springer. pp. 239–246. doi: 10.1007/978-1-4613-8431-1_8 .
↑ Rudin, Mary Ellen (1958). "An unshellable triangulation of a tetrahedron". Bulletin of the American Mathematical Society . 64 (3): 90–91. doi: 10.1090/s0002-9904-1958-10168-8 . ISSN 1088-9485.

Related Research Articles

<span class="mw-page-title-main">Simplex</span> Multi-dimensional generalization of triangle

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,

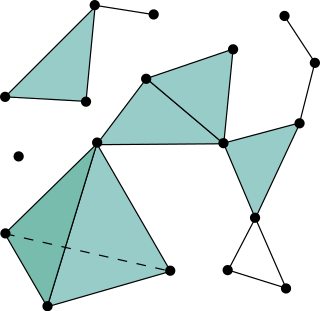
In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial complex from an abstract simplicial complex, the former is often called a geometric simplicial complex.

In mathematics, a building is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces. Buildings were initially introduced by Jacques Tits as a means to understand the structure of isotropic reductive linear algebraic groups over arbitrary fields. The more specialized theory of Bruhat–Tits buildings plays a role in the study of $p$ -adic Lie groups analogous to that of the theory of symmetric spaces in the theory of Lie groups.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or $j$ -faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension $j \leq n$ .

In mathematics, the barycentric subdivision is a standard way to subdivide a given simplex into smaller ones. Its extension on simplicial complexes is a canonical method to refine them. Therefore, the barycentric subdivision is an important tool in algebraic topology.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

In mathematics, a simplicial set is an object composed of simplices in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. Formally, a simplicial set may be defined as a contravariant functor from the simplex category to the category of sets. Simplicial sets were introduced in 1950 by Samuel Eilenberg and Joseph A. Zilber.

In algebraic topology, simplicial homology is the sequence of homology groups of a simplicial complex. It formalizes the idea of the number of holes of a given dimension in the complex. This generalizes the number of connected components.

<span class="mw-page-title-main">Triangulation (topology)</span>

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.

In geometry, a facet is a feature of a polyhedron, polytope, or related geometric structure, generally of dimension one less than the structure itself. More specifically:

In geometry, a simplicial polytope is a polytope whose facets are all simplices. For example, a simplicial polyhedron in three dimensions contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph.

In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial sets. Kan fibrations are the fibrations of the standard model category structure on simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant objects in this model category. The name is in honor of Daniel Kan.

In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form. A characterization of the set of h-vectors of simplicial polytopes was conjectured by Peter McMullen and proved by Lou Billera and Carl W. Lee and Richard Stanley (g-theorem). The definition of h-vector applies to arbitrary abstract simplicial complexes. The g-conjecture stated that for simplicial spheres, all possible h-vectors occur already among the h-vectors of the boundaries of convex simplicial polytopes. It was proven in December 2018 by Karim Adiprasito.

In mathematics, a Δ-set, often called a Δ-complex or a semi-simplicial set, is a combinatorial object that is useful in the construction and triangulation of topological spaces, and also in the computation of related algebraic invariants of such spaces. A Δ-set is somewhat more general than a simplicial complex, yet not quite as sophisticated as a simplicial set. Simplicial sets have additional structure, so that every simplicial set is also a semi-simplicial set.

In geometry, a Schläfli orthoscheme is a type of simplex. The orthoscheme is the generalization of the right triangle to simplex figures of any number of dimensions. Orthoschemes are defined by a sequence of edges $that are mutually orthogonal. They were introduced by Ludwig Schläfli, who called them orthoschemes and studied their volume in Euclidean, hyperbolic, and spherical geometries. H. S. M. Coxeter later named them after Schläfli. As right triangles provide the basis for trigonometry, orthoschemes form the basis of a trigonometry of n dimensions, as developed by Schoute who called it polygonometry . J.-P. Sydler and Børge Jessen studied orthoschemes extensively in connection with Hilbert's third problem.$

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.

In mathematics, a Stanley–Reisner ring, or face ring, is a quotient of a polynomial algebra over a field by a square-free monomial ideal. Such ideals are described more geometrically in terms of finite simplicial complexes. The Stanley–Reisner ring construction is a basic tool within algebraic combinatorics and combinatorial commutative algebra. Its properties were investigated by Richard Stanley, Melvin Hochster, and Gerald Reisner in the early 1970s.

In mathematics, a cyclic polytope, denoted C(n, d), is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in R^d, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others. They play an important role in polyhedral combinatorics: according to the upper bound theorem, proved by Peter McMullen and Richard Stanley, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number f_i of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.

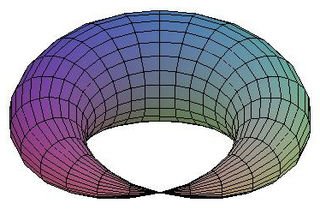
In mathematics, a pseudomanifold is a special type of topological space. It looks like a manifold at most of its points, but it may contain singularities. For example, the cone of solutions of $forms a pseudomanifold.$

Discrete calculus or the calculus of discrete functions, is the mathematical study of incremental change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. The word calculus is a Latin word, meaning originally "small pebble"; as such pebbles were used for calculation, the meaning of the word has evolved and today usually means a method of computation. Meanwhile, calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the study of continuous change.

References

Kozlov, Dmitry (2008). Combinatorial Algebraic Topology. Berlin: Springer. ISBN 978-3-540-71961-8.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Björner, Anders (1984). "Some combinatorial and algebraic properties of Coxeter complexes and Tits buildings". Advances in Mathematics . 52 (3): 173–212. doi: 10.1016/0001-8708(84)90021-5 . ISSN 0001-8708.

[2] Bruggesser, H.; Mani, P. "Shellable Decompositions of Cells and Spheres". Mathematica Scandinavica. 29: 197–205. doi: 10.7146/math.scand.a-11045 .

[3] Ziegler, Günter M. "8.2. Shelling polytopes". Lectures on polytopes. Springer. pp. 239–246. doi: 10.1007/978-1-4613-8431-1_8 .

[4] Rudin, Mary Ellen (1958). "An unshellable triangulation of a tetrahedron". Bulletin of the American Mathematical Society . 64 (3): 90–91. doi: 10.1090/s0002-9904-1958-10168-8 . ISSN 1088-9485.

[1]

[2]

[3]

[4]