In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation, or, equivalently,
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem. In one dimension, it is equivalent to the fundamental theorem of calculus. In three dimensions, it is equivalent to the divergence theorem.
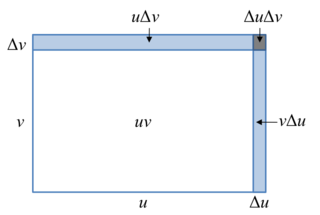
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as or in Leibniz's notation as

In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947; according to Douglas, the functional form itself was developed earlier by Philip Wicksteed.

In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written

In microeconomics, the law of demand is a fundamental principle which states that there is an inverse relationship between price and quantity demanded. In other words, "conditional on all else being equal, as the price of a good increases (↑), quantity demanded will decrease (↓); conversely, as the price of a good decreases (↓), quantity demanded will increase (↑)". Alfred Marshall worded this as: "When we say that a person's demand for anything increases, we mean that he will buy more of it than he would before at the same price, and that he will buy as much of it as before at a higher price". The law of demand, however, only makes a qualitative statement in the sense that it describes the direction of change in the amount of quantity demanded but not the magnitude of change.
In microeconomics, a consumer's Marshallian demand function is the quantity they demand of a particular good as a function of its price, their income, and the prices of other goods, a more technical exposition of the standard demand function. It is a solution to the utility maximization problem of how the consumer can maximize their utility for given income and prices. A synonymous term is uncompensated demand function, because when the price rises the consumer is not compensated with higher nominal income for the fall in their real income, unlike in the Hicksian demand function. Thus the change in quantity demanded is a combination of a substitution effect and a wealth effect. Although Marshallian demand is in the context of partial equilibrium theory, it is sometimes called Walrasian demand as used in general equilibrium theory.
In microeconomics, the expenditure function gives the minimum amount of money an individual needs to spend to achieve some level of utility, given a utility function and the prices of the available goods.
In microeconomics, the expenditure minimization problem is the dual of the utility maximization problem: "how much money do I need to reach a certain level of happiness?". This question comes in two parts. Given a consumer's utility function, prices, and a utility target,
In microeconomics, the Slutsky equation, named after Eugen Slutsky, relates changes in Marshallian (uncompensated) demand to changes in Hicksian (compensated) demand, which is known as such since it compensates to maintain a fixed level of utility.
In economics, a consumer's indirect utility function gives the consumer's maximal attainable utility when faced with a vector of goods prices and an amount of income . It reflects both the consumer's preferences and market conditions.
In microeconomics, a consumer's Hicksian demand function or compensated demand function for a good is their quantity demanded as part of the solution to minimizing their expenditure on all goods while delivering a fixed level of utility. Essentially, a Hicksian demand function shows how an economic agent would react to the change in the price of a good, if the agent's income was compensated to guarantee the agent the same utility previous to the change in the price of the good—the agent will remain on the same indifference curve before and after the change in the price of the good. The function is named after John Hicks.
Roy's identity is a major result in microeconomics having applications in consumer choice and the theory of the firm. The lemma relates the ordinary (Marshallian) demand function to the derivatives of the indirect utility function. Specifically, denoting the indirect utility function as the Marshallian demand function for good can be calculated as
Hotelling's lemma is a result in microeconomics that relates the supply of a good to the maximum profit of the producer. It was first shown by Harold Hotelling, and is widely used in the theory of the firm.
The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
In economics the generalized-Ozaki (GO) cost function is a general description of the cost of production proposed by Shinichiro Nakamura. The GO cost function is notable for explicitly considering nonhomothetic technology, where the proportions of inputs can vary as the output changes. This stands in contrast to the standard production model, which assumes homothetic technology.

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence:
The Almost Ideal Demand System (AIDS) is a consumer demand model used primarily by economists to study consumer behavior. The AIDS model gives an arbitrary second-order approximation to any demand system and has many desirable qualities of demand systems. For instance it satisfies the axioms of order, aggregates over consumers without invoking parallel linear Engel curves, is consistent with budget constraints, and is simple to estimate.
In microeconomic theory, the problem of the integrability of demand functions deals with recovering a utility function from a given walrasian demand function. The "integrability" in the name comes from the fact that demand functions can be shown to satisfy a system of partial differential equations in prices, and solving (integrating) this system is a crucial step in recovering the underlying utility function generating demand.




















