
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B:
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as a three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorove, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.
In mathematics, Hilbert's fourth problem in the 1900 list of Hilbert's problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint.
In mathematics, a complex reflection group is a finite group acting on a finite-dimensional complex vector space that is generated by complex reflections: non-trivial elements that fix a complex hyperplane pointwise.
In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).
In mathematics, the Loomis–Whitney inequality is a result in geometry, which in its simplest form, allows one to estimate the "size" of a -dimensional set by the sizes of its -dimensional projections. The inequality has applications in incidence geometry, the study of so-called "lattice animals", and other areas.
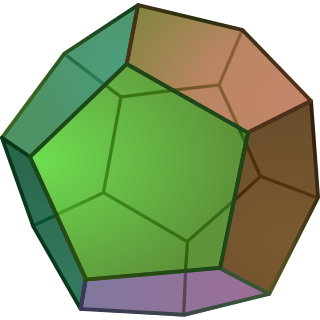
In mathematics, a convex body in -dimensional Euclidean space is a compact convex set with non-empty interior. Some authors do not require a non-empty interior, merely that the set is non-empty.
In mathematics, Minkowski's first inequality for convex bodies is a geometrical result due to the German mathematician Hermann Minkowski. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality.
In mathematics, Busemann's theorem is a theorem in Euclidean geometry and geometric tomography. It was first proved by Herbert Busemann in 1949 and was motivated by his theory of area in Finsler spaces.
In mathematics, particularly, in asymptotic convex geometry, Milman's reverse Brunn–Minkowski inequality is a result due to Vitali Milman that provides a reverse inequality to the famous Brunn–Minkowski inequality for convex bodies in n-dimensional Euclidean space Rn. Namely, it bounds the volume of the Minkowski sum of two bodies from above in terms of the volumes of the bodies.
In convex geometry, the Mahler volume of a centrally symmetric convex body is a dimensionless quantity that is associated with the body and is invariant under linear transformations. It is named after German-English mathematician Kurt Mahler. It is known that the shapes with the largest possible Mahler volume are the balls and solid ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube.
In the mathematical field of convex geometry, the Busemann–Petty problem, introduced by Herbert Busemann and Clinton Myers Petty, asks whether it is true that a symmetric convex body with larger central hyperplane sections has larger volume. More precisely, if K, T are symmetric convex bodies in Rn such that
In convex geometry, the projection body of a convex body in n-dimensional Euclidean space is the convex body such that for any vector , the support function of in the direction u is the (n – 1)-dimensional volume of the projection of K onto the hyperplane orthogonal to u.
In mathematics, the theory of finite sphere packing concerns the question of how a finite number of equally-sized spheres can be most efficiently packed. The question of packing finitely many spheres has only been investigated in detail in recent decades, with much of the groundwork being laid by László Fejes Tóth.






