 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages)
|
In control engineering, a single-input and single-output (SISO) system is a simple single-variable control system with one input and one output. In radio, it is the use of only one antenna both in the transmitter and receiver.
SISO systems are typically less complex than multiple-input multiple-output (MIMO) systems. Usually, it is also easier to make an order of magnitude or trending predictions "on the fly" or "back of the envelope". MIMO systems have too many interactions for most of us to trace through them quickly, thoroughly, and effectively in our heads.
Frequency domain techniques for analysis and controller design dominate SISO control system theory. Bode plot, Nyquist stability criterion, Nichols plot, and root locus are the usual tools for SISO system analysis. Controllers can be designed through the polynomial design, root locus design methods to name just two of the more popular. Often SISO controllers will be PI, PID, or lead-lag.
Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
System analysis in the field of electrical engineering characterizes electrical systems and their properties. System analysis can be used to represent almost anything from population growth to audio speakers; electrical engineers often use it because of its direct relevance to many areas of their discipline, most notably signal processing, communication systems and control systems.
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process.
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters.
H∞methods are used in control theory to synthesize controllers to achieve stabilization with guaranteed performance. To use H∞ methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. H∞ techniques have the advantage over classical control techniques in that H∞ techniques are readily applicable to problems involving multivariate systems with cross-coupling between channels; disadvantages of H∞ techniques include the level of mathematical understanding needed to apply them successfully and the need for a reasonably good model of the system to be controlled. It is important to keep in mind that the resulting controller is only optimal with respect to the prescribed cost function and does not necessarily represent the best controller in terms of the usual performance measures used to evaluate controllers such as settling time, energy expended, etc. Also, non-linear constraints such as saturation are generally not well-handled. These methods were introduced into control theory in the late 1970s-early 1980s by George Zames, J. William Helton , and Allen Tannenbaum.
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex s-plane as a function of a gain parameter.
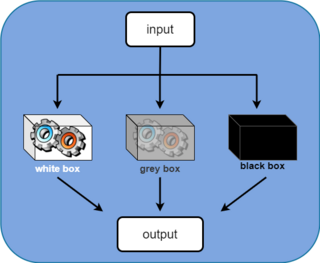
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
A closed-loop controller or feedback controller is a control loop which incorporates feedback, in contrast to an open-loop controller or non-feedback controller. A closed-loop controller uses feedback to control states or outputs of a dynamical system. Its name comes from the information path in the system: process inputs have an effect on the process outputs, which is measured with sensors and processed by the controller; the result is "fed back" as input to the process, closing the loop.
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems.
In control theory, quantitative feedback theory (QFT), developed by Isaac Horowitz, is a frequency domain technique utilising the Nichols chart (NC) in order to achieve a desired robust design over a specified region of plant uncertainty. Desired time-domain responses are translated into frequency domain tolerances, which lead to bounds on the loop transmission function. The design process is highly transparent, allowing a designer to see what trade-offs are necessary to achieve a desired performance level.
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned with the behavior of dynamical systems with inputs, and how to modify the output by changes in the input using feedback, feedforward, or signal filtering. The system to be controlled is called the "plant". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback to the plant to modify the output to bring it closer to the desired output.
In systems theory, closed-loop poles are the positions of the poles of a closed-loop transfer function in the s-plane. The open-loop transfer function is equal to the product of all transfer function blocks in the forward path in the block diagram. The closed-loop transfer function is obtained by dividing the open-loop transfer function by the sum of one and the product of all transfer function blocks throughout the negative feedback loop. The closed-loop transfer function may also be obtained by algebraic or block diagram manipulation. Once the closed-loop transfer function is obtained for the system, the closed-loop poles are obtained by solving the characteristic equation. The characteristic equation is nothing more than setting the denominator of the closed-loop transfer function to zero.
Modal analysis is the study of the dynamic properties of systems in the frequency domain. It consists of mechanically exciting a studied component in such a way to target the modeshapes of the structure, and recording the vibration data with a network of sensors. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeaker.
In radio, multiple-input and multiple-output (MIMO) is a method for multiplying the capacity of a radio link using multiple transmission and receiving antennas to exploit multipath propagation. MIMO has become an essential element of wireless communication standards including IEEE 802.11n, IEEE 802.11ac, HSPA+ (3G), WiMAX, and Long Term Evolution (LTE). More recently, MIMO has been applied to power-line communication for three-wire installations as part of the ITU G.hn standard and of the HomePlug AV2 specification.
In control theory the Youla–Kučera parametrization is a formula that describes all possible stabilizing feedback controllers for a given plant P, as function of a single parameter Q.
The following outline is provided as an overview of and topical guide to control engineering:
Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.
In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.
Per-user unitary rate control (PU2RC) is a multi-user MIMO (multiple-input and multiple-output) scheme. PU2RC uses both transmission pre-coding and multi-user scheduling. By doing that, the network capacity is further enhanced than the capacity of the single-user MIMO scheme.
In mathematics, zero dynamics is known as the concept of evaluating the effect of zero on systems.
 | This engineering-related article is a stub. You can help Wikipedia by expanding it. |
