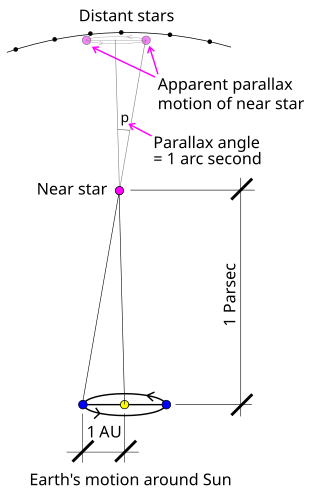
The parsec is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (AU), i.e. 30.9 trillion kilometres. The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 AU subtends an angle of one arcsecond. The nearest star, Proxima Centauri, is about 1.3 parsecs from the Sun: from that distance, the gap between the Earth and the Sun spans slightly less than 1/3600 of one degree of view. Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand parsecs, and the Andromeda Galaxy at over 700 thousand parsecs.

In particle physics, Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction. It is a physical phenomenon explained by Ernest Rutherford in 1911 that led to the development of the planetary Rutherford model of the atom and eventually the Bohr model. Rutherford scattering was first referred to as Coulomb scattering because it relies only upon the static electric (Coulomb) potential, and the minimum distance between particles is set entirely by this potential. The classical Rutherford scattering process of alpha particles against gold nuclei is an example of "elastic scattering" because neither the alpha particles nor the gold nuclei are internally excited. The Rutherford formula further neglects the recoil kinetic energy of the massive target nucleus.

The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless SI derived unit, defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as rad = m/m. Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.

Stellar parallax is the apparent shift of position (parallax) of any nearby star against the background of distant stars. By extension, it is a method for determining the distance to the star through trigonometry, the stellar parallax method. Created by the different orbital positions of Earth, the extremely small observed shift is largest at time intervals of about six months, when Earth arrives at opposite sides of the Sun in its orbit, giving a baseline distance of about two astronomical units between observations. The parallax itself is considered to be half of this maximum, about equivalent to the observational shift that would occur due to the different positions of Earth and the Sun, a baseline of one astronomical unit (AU).

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.

In geometry, a circular segment, also known as a disk segment, is a region of a disk which is "cut off" from the rest of the disk by a secant or a chord. More formally, a circular segment is a region of two-dimensional space that is bounded by a circular arc and by the circular chord connecting the endpoints of the arc.

In optics, the Airy disk and Airy pattern are descriptions of the best-focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
On Sizes and Distances (of the Sun and Moon) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon) is a text by the ancient Greek astronomer Hipparchus (c. 190 – c. 120 BC) in which approximations are made for the radii of the Sun and the Moon as well as their distances from the Earth. It is not extant, but some of its contents have been preserved in the works of Ptolemy and his commentator Pappus of Alexandria. Several modern historians have attempted to reconstruct the methods of Hipparchus using the available texts.
Angular distance or angular separation is the measure of the angle between the orientation of two straight lines, rays, or vectors in three-dimensional space, or the central angle subtended by the radii through two points on a sphere. When the rays are lines of sight from an observer to two points in space, it is known as the apparent distance or apparent separation.

In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted simply as and .

A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to

In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.

The contrast transfer function (CTF) mathematically describes how aberrations in a transmission electron microscope (TEM) modify the image of a sample. This contrast transfer function (CTF) sets the resolution of high-resolution transmission electron microscopy (HRTEM), also known as phase contrast TEM.
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle.


























