 | The article's lead section may need to be rewritten.(September 2021) |
A spherometer is an instrument used for the precise measurement of the radius of curvature of a curved surface. Originally, these instruments were primarily used by opticians to measure the curvature of the surface of a lens. [1]
A spherometer usually consists of:
On new spherometers, the vertical scale is marked off in units of 0.5 mm. One complete turn of the dial also corresponds to 0.5 mm and each small graduation on the dial represents 0.005 mm. The graduations on old spherometers are 0.001 mm.
To measure the radius of a sphere—e.g. the curvature of a lens—the spherometer is leveled and read, then placed on the sphere, adjusted until the four points exert equal pressure, and read again. The difference gives the thickness of that portion of the sphere cut off by a plane passing through the three feet. A contact-lever, delicate level or electric contact may be attached to the spherometer in order to indicate the moment at which the four points exert equal pressure.
The spherometer directly measures a sagitta, h. If the mean length between two outer legs is a, the spherical radius R is given by the formula
Using a spherometer with a circle cup of diameter D, the spherical radius R is instead given by the formula
Since the spherometer is essentially a type of micrometer, it can be employed for purposes other than measuring the curvature of a spherical surface. For example, it can be used to measure the thickness of a thin plate.
To do so, the instrument is placed on a perfectly level plane surface and the screw turned until the point just touches; the exact instant when it does so is defined by a sudden diminution of resistance followed by a considerable increase. The dial and scale are read, the screw is raised, the thin plate slipped under it, and the process is repeated. The difference between the two readings gives the required thickness.
Similarly, the instrument can measure the depression in an otherwise flat plate. The method is as for measuring the thickness of a plate, except that the micrometer portion is placed over the depression and the measurement is taken below the surface instead of above.
This type of instrument is commonly used in inspecting oil field tool pipe for metal surface pits, fractures, and roundness before being shipped to drilling sites for exploratory wells, so that weakened drill pipe will not fracture during drilling. [2] Tool pipe with thicker than 1" walls for a 4" diameter tube of hardened steel, fitted with tapered thread collars, are re-used after drilling is complete and thinner-walled tubular oil-well casing is in place. Electronic instruments similar to the spherometer in design are used at inspection plants for casing, tubing, and drill pipe. The equivalent measurements in optics would be for a cylinder, or lens with a cylindrical component having an optical axis, where a plane through the lens would produce an oval circumference.
An alternate approach using coordinate geometry was developed recently[ citation needed ]. This approach reproduces the well-known result for the spherometer and also leads to a scheme to study aspherical surfaces.
A related device is the cylindrometer (also known as cylindro-spherometer or sphero-cylindrometer), which can additionally measure the radius of curvature of a right-circular cylinder.
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements), usually arranged along a common axis. Lenses are made from materials such as glass or plastic and are ground, polished, or molded to the required shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called "lenses", such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses.
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
A viscometer is an instrument used to measure the viscosity of a fluid. For liquids with viscosities which vary with flow conditions, an instrument called a rheometer is used. Thus, a rheometer can be considered as a special type of viscometer. Viscometers can measure only constant viscosity, that is, viscosity that does not change with flow conditions.
A micrometer, sometimes known as a micrometer screw gauge, is a device incorporating a calibrated screw widely used for accurate measurement of components in mechanical engineering and machining as well as most mechanical trades, along with other metrological instruments such as dial, vernier, and digital calipers. Micrometers are usually, but not always, in the form of calipers. The spindle is a very accurately machined screw and the object to be measured is placed between the spindle and the anvil. The spindle is moved by turning the ratchet knob or thimble until the object to be measured is lightly touched by both the spindle and the anvil.
The focal length of an optical system is a measure of how strongly the system converges or diverges light; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges light. A system with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter distance or diverging them more quickly. For the special case of a thin lens in air, a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in front of the lens a point source must be located to form a collimated beam. For more general optical systems, the focal length has no intuitive meaning; it is simply the inverse of the system's optical power.
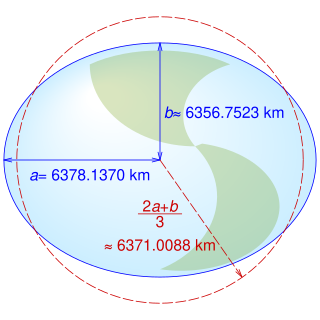
Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).
In optics, spherical aberration (SA) is a type of aberration found in optical systems that have elements with spherical surfaces. Lenses and curved mirrors are prime examples, because this shape is easier to manufacture. Light rays that strike a spherical surface off-centre are refracted or reflected more or less than those that strike close to the centre. This deviation reduces the quality of images produced by optical systems. The effect of spherical aberration was first identified by Ibn al-Haytham who discussed it in his work Kitāb al-Manāẓir.
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.
Caliper(s) or calliper(s) are an instrument used to measure the dimensions of an object; namely, the diameter or depth of a hole. The word “Caliper” comes from latin roots meaning precise pincer.
In various contexts of science, technology, and manufacturing, an indicator is any of various instruments used to accurately measure small distances and angles, and amplify them to make them more obvious. The name comes from the concept of indicating to the user that which their naked eye cannot discern; such as the presence, or exact quantity, of some small distance.
The Surface Force Apparatus (SFA) is a scientific instrument which measures the interaction force of two surfaces as they are brought together and retracted using multiple beam interferometry to monitor surface separation and directly measure contact area and observe any surface deformations occurring in the contact zone. One surface is held by a cantilevered spring, and the deflection of the spring is used to calculate the force being exerted. The technique was pioneered by David Tabor and R.H.S. Winterton in the late 1960s at Cambridge University. By the mid-1970s, J.N. Israelachvili had adapted the original design to operate in liquids, notably aqueous solutions, while at the Australian National University, and further advanced the technique to support friction and electro-chemical surface studies while at the University of California Santa Barbara.
An aspheric lens or asphere is a lens whose surface profiles are not portions of a sphere or cylinder. In photography, a lens assembly that includes an aspheric element is often called an aspherical lens.
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection.
Roundness is the measure of how closely the shape of an object approaches that of a mathematically perfect circle. Roundness applies in two dimensions, such as the cross sectional circles along a cylindrical object such as a shaft or a cylindrical roller for a bearing. In geometric dimensioning and tolerancing, control of a cylinder can also include its fidelity to the longitudinal axis, yielding cylindricity. The analogue of roundness in three dimensions is sphericity.
A lens clock is a mechanical dial indicator that is used to measure the dioptric power of a lens. It is a specialized version of a spherometer. A lens clock measures the curvature of a surface, but gives the result as an optical power in diopters, assuming the lens is made of a material with a particular refractive index.
A toric lens is a lens with different optical power and focal length in two orientations perpendicular to each other. One of the lens surfaces is shaped like a "cap" from a torus, and the other one is usually spherical. Such a lens behaves like a combination of a spherical lens and a cylindrical lens. Toric lenses are used primarily in eyeglasses, contact lenses and intraocular lenses to correct astigmatism.
In materials science and biology, capillary condensation is the "process by which multilayer adsorption from the vapor [phase] into a porous medium proceeds to the point at which pore spaces become filled with condensed liquid from the vapor [phase]." The unique aspect of capillary condensation is that vapor condensation occurs below the saturation vapor pressure, Psat, of the pure liquid. This result is due to an increased number of van der Waals interactions between vapor phase molecules inside the confined space of a capillary. Once condensation has occurred, a meniscus immediately forms at the liquid-vapor interface which allows for equilibrium below the saturation vapor pressure. Meniscus formation is dependent on the surface tension of the liquid and the shape of the capillary, as shown by the Young-Laplace equation. As with any liquid-vapor interface involving a meniscus, the Kelvin equation provides a relation for the difference between the equilibrium vapor pressure and the saturation vapor pressure. A capillary does not necessarily have to be a tubular, closed shape, but can be any confined space with respect to its surroundings.
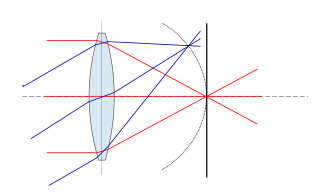
Petzval field curvature, named for Joseph Petzval, describes the optical aberration in which a flat object normal to the optical axis cannot be brought properly into focus on a flat image plane. Field curvature can be corrected with the use of a field flattener, designs can also incorporate a curved focal plane like in the case of the human eye in order to improve image quality at the focal surface.
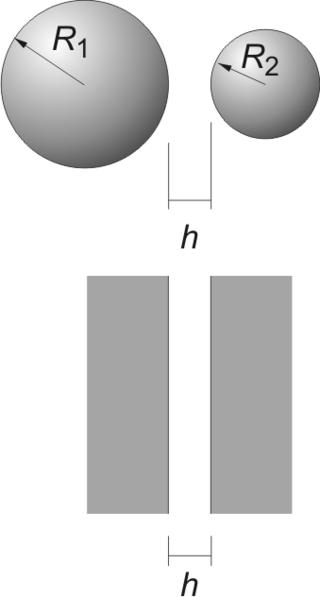
The Derjaguin approximation (or sometimes also referred to as the proximity approximation), named after the Russian scientist Boris Derjaguin, expresses the force profile acting between finite size bodies in terms of the force profile between two planar semi-infinite walls. This approximation is widely used to estimate forces between colloidal particles, as forces between two planar bodies are often much easier to calculate. The Derjaguin approximation expresses the force F(h) between two bodies as a function of the surface separation as
A ball lens is an optical lens in the shape of a sphere. Formally, it is a bi-convex spherical lens with the same radius of curvature on both sides, and diameter equal to twice the radius of curvature. The same optical laws may be applied to analyze its imaging characteristics as for other lenses.
