
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word homeomorphism comes from the Greek words ὅμοιος (homoios) = similar or same and μορφή (morphē) = shape or form, introduced to mathematics by Henri Poincaré in 1895.
In mathematics, a metric space is a set together with a metric on the set. The metric is a function that defines a concept of distance between any two members of the set, which are usually called points. The metric satisfies the following properties:
The Nash embedding theorems, named after John Forbes Nash Jr., state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path. For instance, bending but neither stretching nor tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.

In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the Lipschitz constant of the function. For instance, every function that has bounded first derivatives is Lipschitz continuous.

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective.

High-dimensional data, meaning data that requires more than two or three dimensions to represent, can be difficult to interpret. One approach to simplification is to assume that the data of interest lies within lower-dimensional space. If the data of interest is of low enough dimension, the data can be visualised in the low-dimensional space.
In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance . These maps are the morphisms in the category of metric spaces, Met . They are also called Lipschitz functions with Lipschitz constant 1, nonexpansive maps, nonexpanding maps, weak contractions, or short maps.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the selected segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
In mathematics, a hyperbolic metric space is a metric space satisfying certain metric relations between points. The definition, introduced by Mikhael Gromov, generalizes the metric properties of classical hyperbolic geometry and of trees. Hyperbolicity is a large-scale property, and is very useful to the study of certain infinite groups called Gromov-hyperbolic groups.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or n-manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.
In differential geometry, Mikhail Gromov's filling area conjecture asserts that the hemisphere has minimum area among the orientable surfaces that fill a closed curve of given length without introducing shortcuts between its points.

In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. The property of being quasi-isometric behaves like an equivalence relation on the class of metric spaces.
In mathematics, the Johnson–Lindenstrauss lemma is a result named after William B. Johnson and Joram Lindenstrauss concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. The map used for the embedding is at least Lipschitz, and can even be taken to be an orthogonal projection.

Two-dimensional Euclidean space or simply two-dimensional space is a geometric setting in which two values are required to determine the position of an element on the plane. The set of pairs of real numbers with appropriate structure often serves as the canonical example of a Euclidean plane, the two-dimensional Euclidean space; for a generalization of the concept, see dimension. Two-dimensional space can be seen as a projection of the physical universe onto a plane. Usually, it is thought of as a Euclidean space and the two dimensions are called length and width.

In the mathematical theory of metric spaces, ε-nets, ε-packings, ε-coverings, uniformly discrete sets, relatively dense sets, and Delone sets are several closely related definitions of well-spaced sets of points, and the packing radius and covering radius of these sets measure how well-spaced they are. These sets have applications in coding theory, approximation algorithms, and the theory of quasicrystals.
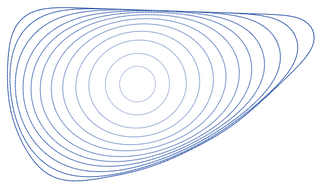
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.

In computational geometry, a greedy geometric spanner is an undirected graph whose distances approximate the Euclidean distances among a finite set of points in a Euclidean space. The vertices of the graph represent these points. The edges of the spanner are selected by a greedy algorithm that includes an edge whenever its two endpoints are not connected by a short path of shorter edges. The greedy spanner was first described in the PhD thesis of Gautam Das and conference paper and subsequent journal paper by Ingo Althöfer et al. These sources also credited Marshall Bern (unpublished) with the independent discovery of the same construction.
In theoretical computer science and metric geometry, the GNRS conjecture connects the theory of graph minors, the stretch factor of embeddings, and the approximation ratio of multi-commodity flow problems. It is named after Anupam Gupta, Ilan Newman, Yuri Rabinovich, and Alistair Sinclair, who formulated it in 2004.










