Subtraction game

Last updated January 14, 2021

In combinatorial game theory, a subtraction game is an abstract strategy game whose state can be represented by a natural number or vector of numbers (for instance, the numbers of game tokens in piles of tokens, or the positions of pieces on board) and in which the allowed moves reduce these numbers.^[1]^[2] Often, the moves of the game allow any number to be reduced by subtracting a value from a specified subtraction set, and different subtraction games vary in their subtraction sets.^[1] These games also vary in whether the last player to move wins (the normal play convention) or loses (misère).^[2] Another winning convention that has also been used is that a player who moves to a position with all numbers zero wins, but that any other position with no moves possible is a draw.^[1]

Examples

Examples of notable subtraction games include the following:

Nim is a game whose state consists of multiple piles of tokens, such as coins or matchsticks, and a valid move removes any number of tokens from a single pile. Nim has a well-known optimal strategy in which the goal at each move is to reach a set of piles whose nim-sum is zero, and this strategy is central to the Sprague–Grundy theorem of optimal play in impartial games. However, when playing only with a single pile of tokens, optimal play is trivial (simply remove all the tokens in a single move).^[3]
Subtract a square is a variation of nim in which only square numbers of tokens can be removed in a single move. The resulting game has a non-trivial strategy even for a single pile of tokens; the Furstenberg–Sárközy theorem implies that its winning positions have density zero among the integers.^[4]
Fibonacci nim is another variation of nim in which the allowed moves depend on the previous moves to the same pile of tokens. On the first move to a pile, it is forbidden to take the whole pile, and on subsequent moves, the amount subtracted must be at most twice the previous amount removed from the same pile.^[5]
Wythoff's game is played by placing a chess queen on a large chessboard and, at each step, moving it (in the normal manner of a chess queen) towards the bottom side, left side, or bottom left corner of the board. This game may be equivalently described with two piles of tokens, from which each move may remove any number of tokens from one or both piles, removing the same amount from each pile when both piles are reduced. It has an optimal strategy involving Beatty sequences and the golden ratio.^[6]

Theory

Subtraction games are generally impartial games, meaning that the set of moves available in a given position does not depend on the player whose turn it is to move. For such a game, the states can be divided up into ${\mathcal {P}}$ -positions (positions in which the previous player, who just moved, is winning) and ${\mathcal {N}}$ -positions (positions in which the next player to move is winning), and an optimal game playing strategy consists of moving to a ${\mathcal {P}}$ -position whenever this is possible. For instance, with the normal play convention and a single pile of tokens, every number in the subtraction set is an ${\mathcal {N}}$ -position, because a player can win from such a number by moving to zero.^[2]

For normal-play subtraction games in which there are multiple numbers, in which each move reduces only one of these numbers, and in which the reductions that are possible from a given number depend only on that number and not on the rest of the game state, the Sprague–Grundy theorem can be used to calculate a "nim value" of each number, a number representing an equivalent position in the game of nim, such that the value of the overall game state is the nim-sum of its nim-values. In this way, the optimal strategy for the overall game can be reduced to the calculation of nim-values for a simplified set of game positions, those in which there is only a single number.^[7] The nim-values are zero for ${\mathcal {P}}$ -positions, and nonzero for ${\mathcal {N}}$ -positions; according to a theorem of Tom Ferguson, the single-number positions with nim-value one are exactly the numbers obtained by adding the smallest value in the subtraction set to a ${\mathcal {P}}$ -position. Ferguson's result leads to an optimal strategy in multi-pile misère subtraction games, with only a small amount of change from the normal play strategy.^[8]

For a subtraction game with a single pile of tokens and a fixed (but possibly infinite) subtraction set, if the subtraction set has arbitrarily large gaps between its members, then the set of ${\mathcal {P}}$ -positions of the game is necessarily infinite.^[9] For every subtraction game with a finite subtraction set, the nim-values are bounded and both the partition into ${\mathcal {P}}$ -positions and ${\mathcal {N}}$ -positions and the sequence of nim-values are eventually periodic. The period may be significantly larger than the maximum value $x$ in the subtraction set, but is at most $2^{x}$ .^[10] However, there exist infinite subtraction sets that produce bounded nim-values but an aperiodic sequence of these values.^[11]

Complexity

For subtraction games with a fixed (but possibly infinite) subtraction set, such as subtract a square, the partition into P-positions and N-positions of the numbers up to a given value $n$ may be computed in time $O(n\log ^{2}n)$ . The nim-values of all numbers up to $n$ may be computed in time $O(\min(ns,nm\log ^{2}n))$ where $s$ denotes the size of the subtraction set (up to $n$ ) and $m$ denotes the largest nim-value occurring in this computation.^[12]

For generalizations of subtraction games, played on vectors of natural numbers with a subtraction set whose vectors can have positive as well as negative coefficients, it is an undecidable problem to determine whether two such games have the same P-positions and N-positions.^[13]

Notes

1 2 3 Golomb (1966).
1 2 3 Berlekamp, Conway & Guy (2001), "Subtraction games", pp. 83–86.
↑ Bouton (1901–1902); Golomb (1966); Berlekamp, Conway & Guy (2001), "Green hackenbush, the game of nim, and nimbers", pp. 40–42.
↑ Golomb (1966); Eppstein (2018)
↑ Whinihan (1963); Larsson & Rubinstein-Salzedo (2016)
↑ Wythoff (1907); Coxeter (1953)
↑ Golomb (1966); Berlekamp, Conway & Guy (2001), "Games with heaps", p. 82.
↑ Ferguson (1974), p. 164; Berlekamp, Conway & Guy (2001), "Ferguson's pairing property", p. 86.
↑ Golomb (1966), Theorem 4.1, p. 451.
↑ Golomb (1966), Example (a), p. 454; Althöfer & Bültermann (1995)
↑ Larsson & Fox (2015).
↑ Eppstein (2018).
↑ Larsson & Wästlund (2013).

Related Research Articles

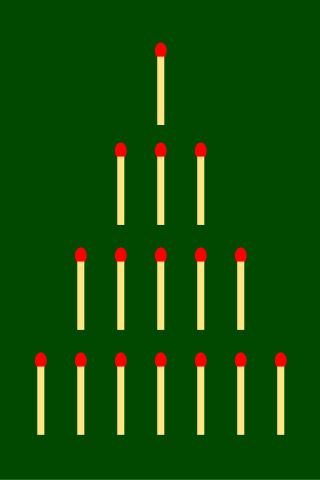
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.

In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a one-heap game of nim, or to an infinite generalization of nim. It can therefore be represented as a natural number, the size of the heap in its equivalent game of nim, as an ordinal number in the infinite generalization, or alternatively as a nimber, the value of that one-heap game in an algebraic system whose addition operation combines multiple heaps to form a single equivalent heap in nim.

In mathematics and computing, Fibonacci coding is a universal code which encodes positive integers into binary code words. It is one example of representations of integers based on Fibonacci numbers. Each code word ends with "11" and contains no other instances of "11" before the end.

In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric. In other words, the only difference between player 1 and player 2 is that player 1 goes first. The game is played until a terminal position is reached. A terminal position is one from which no moves are possible. Then one of the players is declared the winner and the other the loser. Furthermore, impartial games are played with perfect information and no chance moves, meaning all information about the game and operations for both players are visible to both players.

In mathematics, the nimbers, also called Grundy numbers, are introduced in combinatorial game theory, where they are defined as the values of heaps in the game Nim. The nimbers are the ordinal numbers endowed with nimber addition and nimber multiplication, which are distinct from ordinal addition and ordinal multiplication.

Combinatorial game theory (CGT) is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position in which the players take turns changing in defined ways or moves to achieve a defined winning condition. CGT has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.

In combinatorial game theory, star, written as or , is the value given to the game where both players have only the option of moving to the zero game. Star may also be denoted as the surreal form {0|0}. This game is an unconditional first-player win.

In combinatorial game theory, the zero game is the game where neither player has any legal options. Therefore, under the normal play convention, the first player automatically loses, and it is a second-player win. The zero game has a Sprague–Grundy value of zero. The combinatorial notation of the zero game is: { | }.

In mathematics, the mex of a subset of a well-ordered set is the smallest value from the whole set that does not belong to the subset. That is, it is the minimum value of the complement set. The name "mex" is shorthand for "minimum excluded" value.

In mathematics, a Beatty sequence is the sequence of integers found by taking the floor of the positive multiples of a positive irrational number. Beatty sequences are named after Samuel Beatty, who wrote about them in 1926.

Wythoff's game is a two-player mathematical subtraction game, played with two piles of counters. Players take turns removing counters from one or both piles; when removing counters from both piles, the numbers of counters removed from each pile must be equal. The game ends when one person removes the last counter or counters, thus winning.

Subtract-a-square is a two-player mathematical subtraction game. It is played by two people with a pile of coins between them. The players take turns removing coins from the pile, always removing a non-zero square number of coins. The game is usually played as a normal play game, which means that the player who removes the last coin wins. It is an impartial game, meaning that the set of moves available from any position does not depend on whose turn it is. Solomon W. Golomb credits the invention of this game to Richard A. Epstein.

Kayles is a simple impartial game in combinatorial game theory, invented by Henry Dudeney in 1908. Given a row of imagined bowling pins, players take turns to knock out either one pin, or two adjacent pins, until all the pins are gone. Using the notation of octal games, Kayles is denoted 0.77.

The octal games are a class of two-player games that involve removing tokens from heaps of tokens. They have been studied in combinatorial game theory as a generalization of Nim, Kayles, and similar games.

In combinatorial game theory, and particularly in the theory of impartial games in misère play, an indistinguishability quotient is a commutative monoid that generalizes and localizes the Sprague–Grundy theorem for a specific game's rule set.

In combinatorial game theory, poset games are mathematical games of strategy, generalizing many well-known games such as Nim and Chomp. In such games, two players start with a poset, and take turns choosing one point in the poset, removing it and all points that are greater. The player who is left with no point to choose, loses.

In mathematics, the Wythoff array is an infinite matrix of integers derived from the Fibonacci sequence and named after Dutch mathematician Willem Abraham Wythoff. Every positive integer occurs exactly once in the array, and every integer sequence defined by the Fibonacci recurrence can be derived by shifting a row of the array.

The Furstenberg–Sárközy theorem is a result in additive number theory on sets of numbers no two of which differ by a square. It states that, if $is a set of natural numbers with the property that no two numbers in differ by a square number, then the natural density of is zero. That is, for every , and for all sufficiently large , the fraction of the numbers up to that are in is less than . Equivalently, every set of natural numbers with positive upper density contains two numbers whose difference is a square. The theorem is named after Hillel Furstenberg and András Sárközy, who proved it in the late 1970s.$

In number theory, the Moser–de Bruijn sequence is an integer sequence named after Leo Moser and Nicolaas Govert de Bruijn, consisting of the sums of distinct powers of 4. It begins

Fibonacci nim is a mathematical subtraction game, a variant of the game of nim. The game was first described by Michael J. Whinihan in 1963, who credits its invention to Robert E. Gaskell. It is called Fibonacci nim because the Fibonacci numbers feature heavily in its analysis.

References

Althöfer, Ingo; Bültermann, Jörg (1995), "Superlinear period lengths in some subtraction games", Theoretical Computer Science , 148 (1): 111–119, doi:10.1016/0304-3975(95)00019-S, MR 1347670
Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (2001), Winning Ways for your Mathematical Plays, 1 (2nd ed.), A K Peters
Bouton, Charles L. (1901–1902), "Nim, a game with a complete mathematical theory", Annals of Mathematics , Second Series, 3 (1/4): 35–39, doi:10.2307/1967631, JSTOR 1967631
Coxeter, H. S. M. (1953), "The golden section, phyllotaxis, and Wythoff's game", Scripta Mathematica , 19: 135–143, MR 0057548
Eppstein, David (2018), "Faster evaluation of subtraction games", in Ito, Hiro; Leonardi, Stefano; Pagli, Linda; Prencipe, Giuseppe (eds.), Proc. 9th International Conference on Fun with Algorithms (FUN 2018), Leibniz International Proceedings in Informatics (LIPIcs), 100, Dagstuhl, Germany: Schloss Dagstuhl – Leibniz-Zentrum für Informatik, pp. 20:1–20:12, doi:10.4230/lipics.fun.2018.20
Ferguson, T. S. (1974), "On sums of graph games with last player losing", International Journal of Game Theory, 3: 159–167, doi:10.1007/BF01763255, MR 0384169
Golomb, Solomon W. (1966), "A mathematical investigation of games of "take-away"", Journal of Combinatorial Theory , 1: 443–458, doi: 10.1016/S0021-9800(66)80016-9 , MR 0209015
Larsson, Urban; Fox, Nathan (2015), "An aperiodic subtraction game of nim-dimension two" (PDF), Journal of Integer Sequences , 18 (7), Article 15.7.4, arXiv: 1503.05751 , MR 3370791
Larsson, Urban; Rubinstein-Salzedo, Simon (2016), "Grundy values of Fibonacci nim", International Journal of Game Theory, 45 (3): 617–625, arXiv: 1410.0332 , doi:10.1007/s00182-015-0473-y, MR 3538534
Larsson, Urban; Wästlund, Johan (2013), "From heaps of matches to the limits of computability", Electronic Journal of Combinatorics , 20 (3): P41:1–P41:12, arXiv: 1202.0664 , MR 3118949
Whinihan, Michael J. (1963), "Fibonacci nim" (PDF), Fibonacci Quarterly , 1 (4): 9–13
Wythoff, W. A. (1907), "A modification of the game of nim", Nieuw Archief voor Wiskunde, 7 (2): 199–202

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FOOTNOTEGolomb1966-1] 1 2 3 Golomb (1966).

[wwsub-2] 1 2 3 Berlekamp, Conway & Guy (2001), "Subtraction games", pp. 83–86.

[3] Bouton (1901–1902); Golomb (1966); Berlekamp, Conway & Guy (2001), "Green hackenbush, the game of nim, and nimbers", pp. 40–42.

[4] Golomb (1966); Eppstein (2018)

[5] Whinihan (1963); Larsson & Rubinstein-Salzedo (2016)

[6] Wythoff (1907); Coxeter (1953)

[7] Golomb (1966); Berlekamp, Conway & Guy (2001), "Games with heaps", p. 82.

[8] Ferguson (1974), p. 164; Berlekamp, Conway & Guy (2001), "Ferguson's pairing property", p. 86.

[9] Golomb (1966), Theorem 4.1, p. 451.

[10] Golomb (1966), Example (a), p. 454; Althöfer & Bültermann (1995)

[FOOTNOTELarssonFox2015-11] Larsson & Fox (2015).

[FOOTNOTEEppstein2018-12] Eppstein (2018).

[FOOTNOTELarssonWästlund2013-13] Larsson & Wästlund (2013).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]