In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial:

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.
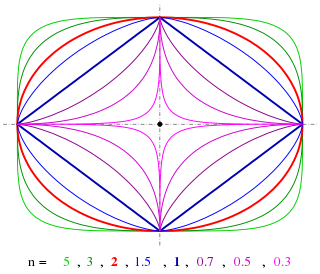
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape.

Piet Hein was a Danish polymath, often writing under the Old Norse pseudonym Kumbel, meaning "tombstone". His short poems, known as gruks or grooks, first started to appear in the daily newspaper Politiken shortly after the German occupation of Denmark in April 1940 under the pseudonym "Kumbel Kumbell". He also invented the Soma cube and the board game Hex.
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

In mathematics, the superquadrics or super-quadrics are a family of geometric shapes defined by formulas that resemble those of ellipsoids and other quadrics, except that the squaring operations are replaced by arbitrary powers. They can be seen as the three-dimensional relatives of the superellipses. The term may refer to the solid object or to its surface, depending on the context. The equations below specify the surface; the solid is specified by replacing the equality signs by less-than-or-equal signs.
In mathematics, a superabundant number is a certain kind of natural number. A natural number n is called superabundant precisely when, for all m < n:
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded in others. They are named after Sergei Lvovich Sobolev.

A squircle is a shape intermediate between a square and a circle. There are at least two definitions of "squircle" in use, the most common of which is based on the superellipse. The word "squircle" is a portmanteau of the words "square" and "circle". Squircles have been applied in design and optics.

In probability theory, the Schramm–Loewner evolution with parameter κ, also known as stochastic Loewner evolution (SLEκ), is a family of random planar curves that have been proven to be the scaling limit of a variety of two-dimensional lattice models in statistical mechanics. Given a parameter κ and a domain in the complex plane U, it gives a family of random curves in U, with κ controlling how much the curve turns. There are two main variants of SLE, chordal SLE which gives a family of random curves from two fixed boundary points, and radial SLE, which gives a family of random curves from a fixed boundary point to a fixed interior point. These curves are defined to satisfy conformal invariance and a domain Markov property.

The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections that may be used for world maps. Waldo R. Tobler introduced the construction in 1973 as the hyperelliptical projection, now usually known as the Tobler hyperelliptical projection.

In mathematics, a superellipsoid is a solid whose horizontal sections are superellipses with the same squareness parameter , and whose vertical sections through the center are superellipses with the squareness parameter . It is a generalization of an ellipsoid, which is a special case when .
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.
In mathematics and physics, Lieb–Thirring inequalities provide an upper bound on the sums of powers of the negative eigenvalues of a Schrödinger operator in terms of integrals of the potential. They are named after E. H. Lieb and W. E. Thirring.

A superparabola is a geometric curve defined in the Cartesian coordinate system as a set of points (x, y) with

















