
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect at exactly one point.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In finite geometry, the Fano plane is the finite projective plane of order 2. It is the finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2) where PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

In geometry an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines through each point. It is not possible to draw points and lines having this pattern of incidences in the Euclidean plane, but it is possible in the complex projective plane.
In mathematics, a regular matroid is a matroid that can be represented over all fields.
In incidence geometry, the De Bruijn–Erdős theorem, originally published by Nicolaas Govert de Bruijn and Paul Erdős (1948), states a lower bound on the number of lines determined by n points in a projective plane. By duality, this is also a bound on the number of intersection points determined by a configuration of lines.
In mathematics, a uniform matroid is a matroid in which the independent sets are exactly the sets containing at most r elements, for some fixed integer r. An alternative definition is that every permutation of the elements is a symmetry.
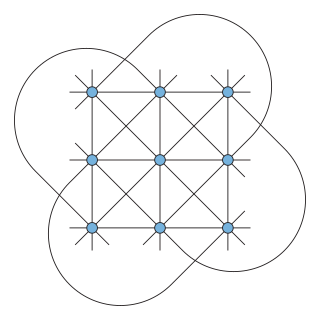
In geometry, the Hesse configuration, introduced by Colin Maclaurin and studied by Hesse (1844), is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane.
In geometry, a Sylvester–Gallai configuration consists of a finite subset of the points of a projective space with the property that the line through any two of the points in the subset also passes through at least one other point of the subset.
Rota's excluded minors conjecture is one of a number of conjectures made by mathematician Gian-Carlo Rota. It is considered to be an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture has been announced by Geelen, Gerards, and Whittle.
In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.












