In Education
| | This section needs expansion. You can help by adding to it. (December 2023) |
Taxman and its variants have been studied and used as tools in mathematics and computer science education. [37] [21] [38] [20] [26] [39]
Taxman, also known as Tax Factor, Number Shark, The Factor Game, Factor Blast, Factor Blaster, or Dr. Factor, is a mathematical game invented by mathematician Diane Resek.
The game is played between two players on a board consisting of whole numbered tokens labeled 1 through N, where N is any positive whole number. During each turn, one player (deemed the tax payer) takes a number from the board, and the other player (deemed the taxman) removes all remaining factors of the tax payer's number from the board. The game ends when there are no legal moves left, and each player's score is calculated by adding up the values of the numbers they have collected. The player with the highest score wins. [1] [2] [3] [4] [5] [6] [7] [8]
In the single-player version, (Taxman, Tax Factor, Number Shark), the human player assumes the role of the tax payer each turn while the computer player is always the taxman. In addition, the human player may only collect a number that still has proper factors remaining on the board. When there are no legal moves left, the taxman collects all of the remaining tokens on the board. [1] [2] [3]
In all two-player versions of the game, (The Factor Game, Factor Blast, Factor Blaster, Dr. Factor), the two players swap roles each turn, so that whoever is playing as the taxman during one turn will be the tax payer during the next turn, and vice versa. [4] [5] [6] [7] [8]
Taxman was invented by Resek sometime in the late 60's or early 70's while working at the Lawrence Hall of Science. [9] It was published as a BASIC program in the September 1973 issue of the People's Computer Company Newsletter , [1] and later appeared in the 1975 programming anthology book What to Do After You Hit Return. [10]
In 1980, Taxman appeared as part of the software collection MECC - Elementary Volume 1 for the Apple II. [11] [12] The concept was later reused in other MECC titles, such as Wonderland Puzzles (as Hedgehog Croquet) and The Secret Island of Dr. Quandary (as Tax Factor) in 1992. [13] [14] [2] [15]
Starting in 1984, Taxman appeared as a coding exercise in a series of programming textbooks written by Lowell Carmony, a professor at Lake Forest College (and Berkeley alumnus). [16] [17] [18] [19] Carmony was part of the writing group for the 1993 NRC publication Measuring Up: Prototypes for Mathematics Assessment, which included Taxman as one of its prototypes. [20] Carmony also described Taxman in an article for SIGCSE. [21]
In 1996, a list of the best possible scores in Taxman, (called the Taxman sequence), was uploaded to the On-Line Encyclopedia of Integer Sequences. [22] As of 2022, the sequence has been calculated out to a board size of 1000. [23]
Around 2000, a version of Taxman was uploaded to the NRW's learn:line educational server under the name Der Zahlenhai (or Number Shark in English). [3] A version of Number Shark was later added to CrypTool in 2006. [24]
In 2015, Taxman appeared in the New York Times' Numberplay column as The Tax Collector. [25]
A two-player version of Taxman, known simply as The Factor Game, was described in an article for the November 1973 issue of The Arithmetic Teacher, a publication of the National Council of Teachers of Mathematics. [26] The article was later reprinted in the 1975 anthology Games and Puzzles for Elementary and Middle School Mathematics. [4]
In 1983, Factor Blast by Joe DeMuth was published by Hayden Software. [27] [5] Around 2000, educator Terry Kawas developed teaching materials for a similar variant called Factor Blaster which was later uploaded to Mathwire, a math education resource website. [28] [6] [29]
In 1985, Dr. Factor appeared as one of four games in Playing To Learn by Antonia Stone, Joshua Abrams, and Ihor Charischak of HRM Software. [30] [31] [7]
In 1986, another variant, also called The Factor Game, appeared as the first activity in the Factors and Multiples module of the Middle Grades Mathematics Project curriculum, and later appeared as part of the Connected Mathematics Project in 1996. [32] [33] [34] Interactive versions were developed for Macintosh and Windows, and eventually a web version was developed for the NCTM's Illuminations website in 2001. [35] [36]
| | This section needs expansion. You can help by adding to it. (December 2023) |
Taxman and its variants have been studied and used as tools in mathematics and computer science education. [37] [21] [38] [20] [26] [39]
| | This section needs expansion. You can help by adding to it. (December 2023) |
The winnability, strategy, and optimal score for the single-player version of Taxman have been studied. [40] [21] [38] [22] [41] [42]

Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of number they operate on. Integer arithmetic restricts itself to calculations with positive and negative whole numbers. Rational number arithmetic involves operations on fractions that lie between integers. Real number arithmetic includes calculations with both rational and irrational numbers and covers the complete number line. Another distinction is based on the numeral system employed to perform calculations. Decimal arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express numbers. Binary arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Some arithmetic systems operate on mathematical objects other than numbers, such as interval arithmetic and matrix arithmetic.
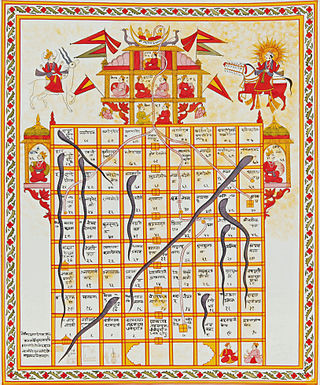
Snakes and ladders is a board game for two or more players regarded today as a worldwide classic. The game originated in ancient India as Moksha Patam, and was brought to the UK in the 1890s. It is played on a game board with numbered, gridded squares. A number of "ladders" and "snakes" are pictured on the board, each connecting two specific board squares. The object of the game is to navigate one's game piece, according to die rolls, from the start to the finish, helped by climbing ladders but hindered by falling down snakes.

The Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to one of the other rods, obeying the following rules:

In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system.

In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is divisible by 2, and odd if it is not divisible. For example, −4, 0, and 82 are even numbers, while −3, 5, 7, and 21 are odd numbers.

The Oregon Trail is a text-based strategy video game developed by Don Rawitsch, Bill Heinemann, and Paul Dillenberger in 1971 and produced by the Minnesota Educational Computing Consortium (MECC) beginning in 1975. It was developed as a computer game to teach school children about the realities of 19th-century pioneer life on the Oregon Trail. In the game, the player assumes the role of a wagon leader guiding a party of settlers from Independence, Missouri, to Oregon City, Oregon via a covered wagon in 1847. Along the way the player must purchase supplies, hunt for food, and make choices on how to proceed along the trail while encountering random events such as storms and wagon breakdowns. The original versions of the game contain no graphics, as they were developed for computers that used teleprinters instead of computer monitors. A later Apple II port added a graphical shooting minigame.

Zoombinis is a series of educational puzzle computer games that were originally developed by TERC and published by Broderbund. In 1998, Broderbund was purchased by The Learning Company, who took responsibility for developing and publishing the series in 2001. The series consists of three games: Logical Journey of the Zoombinis (1996), Zoombinis: Mountain Rescue (2001), and Zoombinis: Island Odyssey (2002). Logical Journey was remade as Zoombinis for modern operating systems in 2015. The series focuses on the Zoombinis, small blue creatures each with different appearances and personalities, which the player must guide through strange puzzle-filled lands.
Verbal arithmetic, also known as alphametics, cryptarithmetic, cryptarithm or word addition, is a type of mathematical game consisting of a mathematical equation among unknown numbers, whose digits are represented by letters of the alphabet. The goal is to identify the value of each letter. The name can be extended to puzzles that use non-alphabetic symbols instead of letters.
The Minnesota Educational Computing Consortium, most commonly known as MECC, was an organization founded in 1971 best known for developing the edutainment video game series The Oregon Trail and its spinoffs. The goal of the organization was to coordinate and provide computer services to schools in the state of Minnesota; however, its software eventually became popular in schools around the world. MECC had its headquarters in the Brookdale Corporate Center in Brooklyn Center, Minnesota. It was acquired by SoftKey in 1995 and was shut down in 1999.

Number Munchers is a 1986 video game and a spin-off to the title Word Munchers. It was made by MECC for Apple II, then ported to DOS and Macintosh in 1990. The concept of the game was designed by R. Philip Bouchard, who also designed The Oregon Trail. Two versions of the game were released the Consumer Version and the School Version. After The Learning Company acquired MECC, the game was rebranded as "Math Munchers".
Principles and Standards for School Mathematics (PSSM) are guidelines produced by the National Council of Teachers of Mathematics (NCTM) in 2000, setting forth recommendations for mathematics educators. They form a national vision for preschool through twelfth grade mathematics education in the US and Canada. It is the primary model for standards-based mathematics.
Munchers is a series of educational/edutainment computer games produced by the Minnesota Educational Computing Consortium (MECC) for several operating systems. The series was popular among American schoolchildren in the 1980s and 1990s and were the recipients of several awards. The two original games in the series were Number Munchers and Word Munchers. The brand name is currently owned by Houghton Mifflin Harcourt, but is defunct.

The Secret Island of Dr. Quandary is an educational computer puzzle game developed by MECC, which pits the player against a variety of mathematical and logical puzzles. It was released in 1992 for MS-DOS and Macintosh.

The SpongeBob SquarePants Movie is a 2004 platform video game based on the film of the same name and published by THQ for the PlayStation 2, Xbox, GameCube, Microsoft Windows, and Game Boy Advance. The PlayStation 2, Xbox, and GameCube versions were developed by Heavy Iron Studios. The Game Boy Advance version was developed by WayForward Technologies. The Microsoft Windows version was developed by AWE Games. The Mac version was developed by Aspyr. Most of the film's cast reprise their roles.
Traditional mathematics was the predominant method of mathematics education in the United States in the early-to-mid 20th century. This contrasts with non-traditional approaches to math education. Traditional mathematics education has been challenged by several reform movements over the last several decades, notably new math, a now largely abandoned and discredited set of alternative methods, and most recently reform or standards-based mathematics based on NCTM standards, which is federally supported and has been widely adopted, but subject to ongoing criticism.
Geometry from the Land of the Incas is a free geometry website funded by advertising, aimed mainly at high school and college age students.
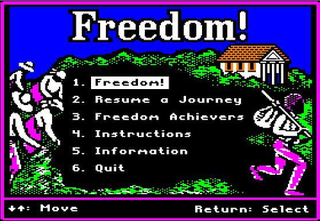
Freedom! is a 1993 educational computer game developed and published by the Minnesota Educational Computing Consortium (MECC). Based on similar gameplay from MECC's earlier The Oregon Trail, the player assumes the role of a runaway slave in the antebellum period of American history who is trying to reach the North through the Underground Railroad. The game was developed with help of an African-American consultant who guided MECC on appropriate graphics and dialect that represented the era. It is recognized as one of the first video games dealing with the topic of slavery.
Frances Ann Novak Rosamond is an Australian computer scientist whose research interests include computer education and parameterized complexity. She is the editor of the Parameterized Complexity Newsletter, moderator of the parameterized complexity wiki, and publicity chair of the International Symposium on Parameterized and Exact Computation.
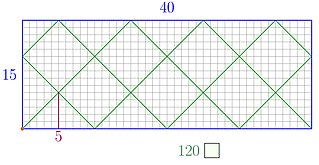
In recreational mathematics, arithmetic billiards provide a geometrical method to determine the least common multiple and the greatest common divisor of two natural numbers by making use of reflections inside a rectangle whose sides are the two given numbers. This is an easy example of trajectory analysis of dynamical billiards.

The Oregon Trail is an educational strategy video game developed and published by the Minnesota Educational Computing Consortium (MECC). It was first released in 1985 for the Apple II, with later ports to DOS in 1990, Mac OS in 1991, and Microsoft Windows in 1993. It was created as a re-imagining of the popular text-based game of the same name, originally created in 1971 and published by MECC in 1975. In the game, the player assumes the role of a wagon leader guiding a party of settlers from Independence, Missouri, to Oregon's Willamette Valley via a covered wagon on the Oregon Trail in 1848. Along the trail, the player makes choices about supplies, resource management, and the route, and deals with hunting for food, crossing rivers, and random events such as storms and disease.
'I'll take some of the tokens from your bag and put them out on the trail. Next, you pick up one of the tokens. Then, I'll pick up all the FACTORS of the token you picked up... High score wins... You can't take that token. No other tokens are factors of that token... That's it! The west are mine!!'
I learned that the game was invented by Diane Resek of San Francisco State University. She writes: 'I came up with the game when I was working at the Lawrence Hall of Science in Berkeley from about 1969 to 1972.'
1. You may take any numbered hedgehog if it has a factor (other than itself) showing. 2. The queen gets all the factors of your number. 3. The queen gets all the leftover hedgehogs.
Kawas, 2000