In physics, a force is an influence that can cause an object to change its velocity, i.e., to accelerate, meaning a change in speed or direction, unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the magnitude and direction of a force are both important, force is a vector quantity. The SI unit of force is the newton (N), and force is often represented by the symbol F.

Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies.

In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. The term potential energy was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to the ancient Greek philosopher Aristotle's concept of potentiality.

An electric field is the physical field that surrounds electrically charged particles. Charged particles exert attractive forces on each other when their charges are opposite, and repulse each other when their charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. The electric field of a single charge describes their capacity to exert such forces on another charged object. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Thus, we may informally say that the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker further away. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, Electromagnetism is one of the four fundamental interactions of nature.

In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.

In physics, the center of mass of a distribution of mass in space is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.
Newton's law of universal gravitation says that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.

In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude of torque the object experiences in a given magnetic field. When the same magnetic field is applied, objects with larger magnetic moments experience larger torques. The strength of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. Its direction points from the south pole to north pole of the magnet.
In physics, the gyromagnetic ratio of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol γ, gamma. Its SI unit is the radian per second per tesla (rad⋅s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1).
A classical field theory is a physical theory that predicts how one or more fields in physics interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.
The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum. This is the steady gain in speed caused exclusively by gravitational attraction. All bodies accelerate in vacuum at the same rate, regardless of the masses or compositions of the bodies; the measurement and analysis of these rates is known as gravimetry.

The mass-to-charge ratio (m/Q) is a physical quantity relating the mass (quantity of matter) and the electric charge of a given particle, expressed in units of kilograms per coulomb (kg/C). It is most widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics.
This article will use the Einstein summation convention.
In physics, relativistic quantum mechanics (RQM) is any Poincaré covariant formulation of quantum mechanics (QM). This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics. Non-relativistic quantum mechanics refers to the mathematical formulation of quantum mechanics applied in the context of Galilean relativity, more specifically quantizing the equations of classical mechanics by replacing dynamical variables by operators. Relativistic quantum mechanics (RQM) is quantum mechanics applied with special relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, a few of them also work with special relativity.

Gravitoelectromagnetism, abbreviated GEM, refers to a set of formal analogies between the equations for electromagnetism and relativistic gravitation; specifically: between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. Gravitomagnetism is a widely used term referring specifically to the kinetic effects of gravity, in analogy to the magnetic effects of moving electric charge. The most common version of GEM is valid only far from isolated sources, and for slowly moving test particles.
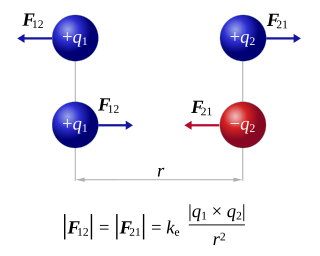
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the electrostatic force or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle.

In physics, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. A weather map, with the surface temperature described by assigning a number to each point on the map, is an example of a scalar field. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.























