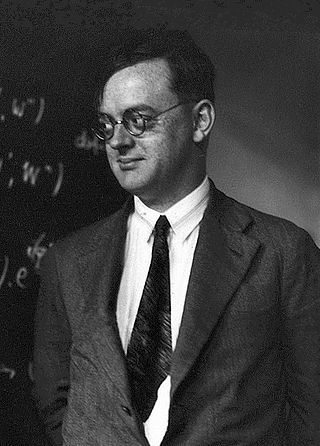Paul Adrien Maurice Dirac was an English mathematical and theoretical physicist who is considered to be one of the founders of quantum mechanics. Dirac laid the foundations for both quantum electrodynamics and quantum field theory. He was the Lucasian Professor of Mathematics at the University of Cambridge, a professor of physics at Florida State University, and a 1933 Nobel Prize in Physics recipient.

Quantum mechanics is a fundamental theory that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.

In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.

Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after having been nominated by Albert Einstein, Pauli received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or Pauli principle". The discovery involved spin theory, which is the basis of a theory of the structure of matter.
A timeline of atomic and subatomic physics, including particle physics.

Julian Seymour Schwinger was a Nobel Prize-winning American theoretical physicist. He is best known for his work on quantum electrodynamics (QED), in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order. Schwinger was a physics professor at several universities.

Renormalization is a collection of techniques in quantum field theory, statistical field theory, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian.

QED: The Strange Theory of Light and Matter is an adaptation for the general reader of four lectures on quantum electrodynamics (QED) published in 1985 by American physicist and Nobel laureate Richard Feynman.
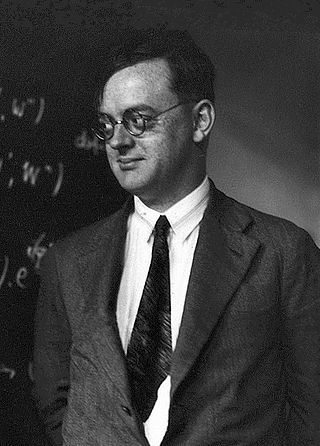
Ernst Pascual Jordan was a German theoretical and mathematical physicist who made significant contributions to quantum mechanics and quantum field theory. He contributed much to the mathematical form of matrix mechanics, and developed canonical anticommutation relations for fermions. He introduced Jordan algebras in an effort to formalize quantum field theory; the algebras have since found numerous applications within mathematics.
In physics, especially quantum field theory, regularization is a method of modifying observables which have singularities in order to make them finite by the introduction of a suitable parameter called the regulator. The regulator, also known as a "cutoff", models our lack of knowledge about physics at unobserved scales. It compensates for the possibility of separation of scales that "new physics" may be discovered at those scales which the present theory is unable to model, while enabling the current theory to give accurate predictions as an "effective theory" within its intended scale of use.

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Major advances in the theory were made in the 1940s and 1950s, leading to the introduction of renormalized quantum electrodynamics (QED). The field theory behind QED was so accurate and successful in predictions that efforts were made to apply the same basic concepts for the other forces of nature. Beginning in 1954, the parallel was found by way of gauge theory, leading by the late 1970s, to quantum field models of strong nuclear force and weak nuclear force, united in the modern Standard Model of particle physics.
Quantum mechanics is the study of matter and its interactions with energy on the scale of atomic and subatomic particles. By contrast, classical physics explains matter and energy only on a scale familiar to human experience, including the behavior of astronomical bodies such as the moon. Classical physics is still used in much of modern science and technology. However, towards the end of the 19th century, scientists discovered phenomena in both the large (macro) and the small (micro) worlds that classical physics could not explain. The desire to resolve inconsistencies between observed phenomena and classical theory led to a revolution in physics, a shift in the original scientific paradigm: the development of quantum mechanics.
The ensemble interpretation of quantum mechanics considers the quantum state description to apply only to an ensemble of similarly prepared systems, rather than supposing that it exhaustively represents an individual physical system.
The history of quantum mechanics is a fundamental part of the history of modern physics. The major chapters of this history begin with the emergence of quantum ideas to explain individual phenomena—blackbody radiation, the photoelectric effect, solar emission spectra—an era called the Old or Older quantum theories. Building on the technology developed in classical mechanics, the invention of wave mechanics by Erwin Schrödinger and expansion by many others triggers the "modern" era beginning around 1925. Paul Dirac's relativistic quantum theory work lead him to explore quantum theories of radiation, culminating in quantum electrodynamics, the first quantum field theory. The history of quantum mechanics continues in the history of quantum field theory. The history of quantum chemistry, theoretical basis of chemical structure, reactivity, and bonding, interlaces with the events discussed in this article.
In the history of physics, "On the quantum-theoretical reinterpretation of kinematical and mechanical relationships" (German: Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen), also known as the Umdeutung (reinterpretation) paper, was a breakthrough article in quantum mechanics written by Werner Heisenberg, which appeared in Zeitschrift für Physik in September 1925.
The Planck constant, or Planck's constant, denoted by , is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The closely related reduced Planck constant, equal to and denoted is commonly used in quantum physics equations.
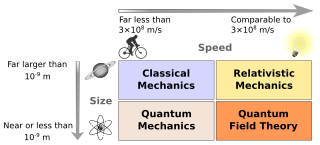
Physics is a scientific discipline that seeks to construct and experimentally test theories of the physical universe. These theories vary in their scope and can be organized into several distinct branches, which are outlined in this article.

In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. An example of a scalar field is a weather map, with the surface temperature described by assigning a number to each point on the map. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.
Laurie Mark Brown is an American theoretical physicist and historian of quantum field theory and elementary particle physics.