Theory of sonics

Last updated May 15, 2024

The theory of sonics is a branch of continuum mechanics which describes the transmission of mechanical energy through vibrations. The birth of the theory of sonics^[1] is the publication of the book A treatise on transmission of power by vibrations in 1918 by the Romanian scientist Gogu Constantinescu.

ONE of the fundamental problems of mechanical engineering is that of transmitting energy found in nature, after suitable transformation, to some point at which can be made available for performing useful work. The methods of transmitting power known and practised by engineers are broadly included in two classes: mechanical including hydraulic, pneumatic and wire rope methods; and electrical methods....According to the new system, energy is transmitted from one point to another, which may be at a considerable distance, by means of impressed variations of pressure or tension producing longitudinal vibrations in solid, liquid or gaseous columns. The energy is transmitted by periodic changes of pressure and volume in the longitudinal direction and may be described as wave transmission of power, or mechanical wave transmission. – Gogu Constantinescu^[2]^[3]

Later on the theory was expanded in electro-sonic, hydro-sonic, sonostereo-sonic and thermo-sonic. The theory was the first chapter of compressible flow applications and has stated for the first time the mathematical theory of compressible fluid, and was considered a branch of continuum mechanics. The laws discovered by Constantinescu, used in sonicity are the same with the laws used in electricity.

Book chapters

The book A treatise on transmission of power by vibrations has the following chapters:

Introductory
Elementary physical principles
Definitions
Effects of capacity, inertia, friction, and leakage on alternating currents
Waves in long pipes
Alternating in long pipes allowing for Friction
Theory of displacements – motors
Theory of resonators
High-frequency currents
Charged lines
Transformers

George Constantinescu defined his work as follow.

Theory of sonics: applications

The Constantinesco synchronization gear, used on military aircraft in order to allow them to target opponents without damaging their own propellers.
Automatic gear
Sonic Drilling, was one of the first applications developed by Constantinescu. A sonic drill head works by sending high frequency resonant vibrations down the drill string to the drill bit, while the operator controls these frequencies to suit the specific conditions of the soil/rock geology.
Torque Converter.^[4] A mechanical application of sonic theory on the transmission of power by vibrations. Power is transmitted from the engine to the output shaft through a system of oscillating levers and inertias.
Sonic Engine

Elementary physical principles

If v is the velocity of which waves travel along the pipe, and n the number of the revolutions of the crank a, then the wavelength λ is:

$\lambda ={\frac {v}{n}}\,$
Assuming that the pipe is finite and closed at the point r situated at a distance which is multiple of λ, and considering that the piston is smaller than wavelength, at r the wave compression is stopped and reflected, the reflected wave traveling back along the pipe.

Physics
Elementary physical principles	Description
Figure I Suppose the crank a to be rotating uniformly, causing the piston b to reciprocate in the pipe c, which is full of liquid. At each in stroke of the piston a zone of high pressure is formed, and these zones, shown by shading, travel along the pipe away from the piston; between every pair of high pressures zones is a zone of low pressure shown in the picture. The pressure at any point in the pipe will go through a series of values from a maximum to a minimum.
Figure II Assuming that the pipe is finite and closed at the point r situated at a distance which is a multiple of λ, and considering that the piston is smaller than the wavelength, at r the wave compression is stopped and reflected, the reflected wave traveling back along the pipe. If the crank continues rotation at a uniform speed, a zone of maximum pressure will start from the piston at the same time the reflected wave returns to the piston. As a result, the maximum pressure will double. At the next rotation the amplitude is increased, and so on, until the pipe bursts.
Figure III If instead of a closed end we have a piston at r; the wave will be similar at piston b and piston m, the piston m therefore will have the same energy as the piston b; if the distance between the b and m is not a multiple of λ, the movement of m will differ in phase compared with the piston b.
Figure IV If more energy is produced by piston b than is taken by piston m, the energy will be reflected by piston m in the pipe, and the energy will accumulate until the pipe bursts. If we have a vessel d, with a large volume compared with the stroke volume of piston b, the capacity d will act as a spring storing the energy of direct or reflected waves at high pressure, and giving back energy when the pressure falls. The mean pressure in d and in the pipe will be the same, but the pipe will have a stationary wave as a result of the reflected waves with no increase of energy, and the pressure in the pipe will never exceed the pressure limit.
Figure V Waves are transmitted by a reciprocating piston along the pipe eeee. The pipe is closed at p, a distance of one complete wavelength. There are branches b, c, and d at distances of one-half, three-quarters and one full wavelength, respectively. If p is open and d is open, the motor l will rotate synchronous with motor a. If all valves are closed, there will be a stationary wave with extreme values at λ and λ/2, (points b and d,) where the flow will be zero, and where the pressure will alternate between maximum and minimum values determined by the capacity of the reservoir f. The maximum and minimum points do not move along the pipe, and no energy flows from generator a. If valve b is open, the motor m is able to take the energy from the line, the stationary half-wave between a and b being replaced by a traveling wave; between b and p a stationary wave will persist. If only valve c is open, since at this point the variation of pressure is always zero, no energy can be taken out by the motor n, and the stationary wave will persist. If the motor is connected in an intermediary point, part of the energy will be taken out by the motor while the stationary wave will persist at reduced amplitude. If the motor l is not capable of consuming all the energy of the generator a, then there will be a combination of traveling waves and stationary waves. Therefore, there will be no point in the pipe where the pressure variation will be zero, and consequently, a motor connected at any point of the pipe will be able to use a portion of generated energy.

Definitions

Alternating fluid currents

Considering any flow or pipes, if:

ω = the area section of the pipe measured in square centimeters;

v = the velocity of the fluid at any moment in centimeters per second;

and

i = the flow of liquid in cubic centimeters per second,

then we have:

i = vω

Assuming that the fluid current is produced by a piston having a simple harmonic movement, in a piston cylinder having a section of Ω square centimeters. If we have:

r = the equivalent of driving crank in centimeters

a = the angular velocity of the crank or the pulsations in radians per second.

n = the number of crank rotations per second.

Then:

The flow from the cylinder to the pipe is: i = Isin(at+φ)

Where:

I = raΩ (the maximum alternating flow in square centimeters per second; the amplitude of the flow.)

t = time in seconds

φ = the angle of the phase

If T= period of a complete alternation (one revolution of the crank) then:

a = 2πn; where n = 1/T

The effective current can be defined by the equation:

I_{eff}^{2}={\frac {1}{T}}\int \limits _{0}^{T}i^{2}\,dt

and the effective velocity is :

v_{eff}={\frac {I_{eff}}{\omega }}

The stroke volume δ will be given by the relation:

\delta =2r\Omega =2{\frac {I}{a}}

Alternating pressures

The alternating pressures are very similar to alternating currents in electricity. In a pipe where the currents are flowing, we will have:

p=H\sin {(at+\Phi )}+p_{m}

; where H is the maximum alternating pressure measured in kilograms per square centimeter.

\Phi =

the angle of phase;

p_{m}

representing the mean pressure in the pipe.

Considering the above formulas:

the minimum pressure is

P_{min}=P_{m}-H

and maximum pressure is

P_{max}=P_{m}+H

If p₁ is the pressure at an arbitrary point and p₂ pressure in another arbitrary point:

The difference

h=p_{1}-p_{2}=H\sin {(at+\Phi )}

is defined as instantaneous hydromotive force between point p₁ and p₂, H representing the amplitude.

The effective hydromotive force will be: $H_{eff}={\frac {H}{\sqrt {2}}}$

Friction

In alternating current flowing through a pipe, there is friction at the surface of the pipe and also in the liquid itself. Therefore, the relation between the hydromotive force and current can be written as:

H=Ri

; where R = coefficient of friction in

{\frac {kg.sec.}{cm.^{5}}}

Using experiments R may be calculated from formula:

R=\epsilon {\frac {\gamma lv_{eff}}{2g\omega d}}

;

Where:

$\gamma$ is the density of the liquid in kg per cm.³
l is the length of the pipe in cm.
g is the gravitational acceleration in cm. per sec.²
$\omega$ is the section of the pipe in square centimeters.
v_eff is the effective velocity
d is the internal diameter of the pipe in centimeters.
$\epsilon =0.02+{\frac {0.18}{\sqrt {v_{eff}d}}}$ for water (an approximation from experimental data).
h is the instantaneous hydromotive force

If we introduce $\epsilon$ in the formula, we get:

R={\frac {\gamma l}{g\omega }}{\big (}0.01{\frac {v}{d}}+{\frac {0.09}{d}}{\sqrt {\frac {v_{eff}}{d}}}{\big )}

which is equivalent to:

100k={\frac {v_{eff}}{d}}+{\frac {9}{d}}{\sqrt {\frac {v_{eff}}{d}}}={\frac {v_{eff}}{d}}{\big (}1+{\frac {9}{v_{eff}}}{\sqrt {\frac {v_{eff}}{d}}}{\big )}

; introducing k in the formula results in

R=k{\frac {\gamma l}{g\omega }}

For pipes with a greater diameter, a greater velocity can be achieved for same value of k. The loss of power due to friction is calculated by:

W={\frac {1}{T}}\int _{0}^{T}hi\,dt

, putting h = Ri results in:

W={\frac {1}{T}}\int _{0}^{T}Ri^{2}\,dt={\frac {R}{T}}\int _{0}^{T}i^{2}\,dt={\frac {RI^{2}}{2}}

Therefore:

W={\frac {RI^{2}}{2}}={\frac {HI}{2}}=H_{eff}\times I_{eff}

Capacity and condensers

Definition: Hydraulic condensers are appliances for making alterations in value of fluid currents, pressures or phases of alternating fluid currents. The apparatus usually consists of a mobile solid body, which divides the liquid column, and is fixed elastically in a middle position such that it follows the movements of the liquid column.

The principal function of hydraulic condensers is to counteract inertia effects due to moving masses.

Hydraulic Condenser Drawing	Theory
Hydraulic Condenser Example $Hooke's law for spring F = m d 2 x d t 2 = - k x {\displaystyle F=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-kx} ; in this case x=f=piston movement. Muelle.gif$ Hooke's law for spring $F=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-kx$ ; in this case x=f=piston movement. Simple Harmonic The principal function of hydraulic condensers is to counteract inertial effects due to moving masses. The capacity C of a condenser consisting of a piston of section ω on which the liquid pressure is acting, held in a mean position by means of springs, is given by the equation: ΔV = ωΔf = CΔp where: ΔV = the variation of volume for the given liquid; Δf = the variation of the longitudinal position of the piston, and Δp = the variation of the pressure in the liquid. If the piston is held by a spring at any given moment: f = AF where A = a constant depending on the spring and F = the force acting on the spring. In the condenser we will have: ΔF = ωΔp and Δf = AωΔp Considering the above equations: C = Aω² and $F={\frac {f}{A}}={\frac {f\omega }{C}}$ For a spring wire of circular section: $B=Ff$ Where B is the volume of spring in cubic centimeters and σ is the allowable stress of metal in kilograms per square centimeter. G is the coefficient of transverse elasticity of the metal. Therefore: B = mFf m being a constant depending on σ and G. If d is the diameter of the spring wire and the D the mean diameter of the spring. Then: $F=0.4{\frac {d^{3}}{D}}\sigma$ so that: $d={\sqrt[{3}]{\frac {FD}{0.4\sigma }}}$ if we consider :: $n={\sqrt[{3}]{\frac {1}{0.4\sigma }}}$ then: $d=n{\sqrt[{3}]{FD}}$ The above equations are used in order to calculate the springs required for a condenser of a given capacity required to work at a given maximum stress.

Notes

↑ "Theory of wave transmission; a treatise on transmission of power by vibrations". 1922.
↑ Constantinesco, G. Theory of Sonics: A Treatise on Transmission of Power by Vibrations. The Admiralty, London, 1918
↑ "Theory of wave transmission; a treatise on transmission of power by vibrations". 1922.
↑ "Archived copy" (PDF). Archived from the original (PDF) on 4 March 2012. Retrieved 17 March 2010.{{cite web}}: CS1 maint: archived copy as title (link)

Related Research Articles

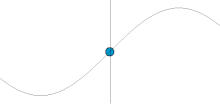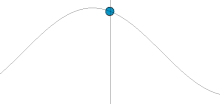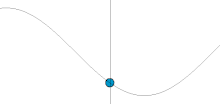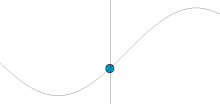
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

<span class="mw-page-title-main">Oscillation</span> Repetitive variation of some measure about a central value

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.

A random variable is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function in which

<span class="mw-page-title-main">Standing wave</span> Wave that remains in a constant position

In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes.

<span class="mw-page-title-main">Navier–Stokes equations</span> Equations describing the motion of viscous fluid substances

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.

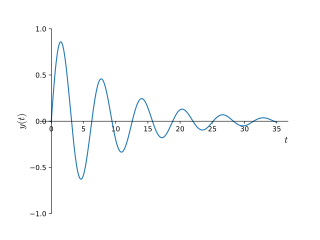
In physics and engineering, the quality factor or Q factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher Q indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high Q, while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer.

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself $as one of the new canonical momentum coordinates.$

<span class="mw-page-title-main">George Constantinescu</span>

George "Gogu" Constantinescu was a Romanian scientist, engineer, and inventor. During his career, he registered over 130 inventions. Constantinescu was the creator of the theory of sonics, a new branch of continuum mechanics, in which he described the transmission of mechanical energy through vibrations.

Chebyshev filters are analog or digital filters that have a steeper roll-off than Butterworth filters, and have either passband ripple or stopband ripple. Chebyshev filters have the property that they minimize the error between the idealized and the actual filter characteristic over the operating frequency range of the filter, but they achieve this with ripples in the passband. This type of filter is named after Pafnuty Chebyshev because its mathematical characteristics are derived from Chebyshev polynomials. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters". Because of the passband ripple inherent in Chebyshev filters, filters with a smoother response in the passband but a more irregular response in the stopband are preferred for certain applications.

<span class="mw-page-title-main">Debye model</span> Method in physics

In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to $- the Debye T 3 law . Similarly to the Einstein photoelectron model, it recovers the Dulong-Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.$

In radio and telecommunications a dipole antenna or doublet is one of the two simplest and most widely-used types of antenna; the other is the monopole. The dipole is any one of a class of antennas producing a radiation pattern approximating that of an elementary electric dipole with a radiating structure supporting a line current so energized that the current has only one node at each far end. A dipole antenna commonly consists of two identical conductive elements such as metal wires or rods. The driving current from the transmitter is applied, or for receiving antennas the output signal to the receiver is taken, between the two halves of the antenna. Each side of the feedline to the transmitter or receiver is connected to one of the conductors. This contrasts with a monopole antenna, which consists of a single rod or conductor with one side of the feedline connected to it, and the other side connected to some type of ground. A common example of a dipole is the "rabbit ears" television antenna found on broadcast television sets. All dipoles are electrically equivalent to two monopoles mounted end-to-end and fed with opposite phases, with the ground plane between them made "virtual" by the opposing monopole.

Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting from an acoustic pressure applied to the system. The SI unit of acoustic impedance is the pascal-second per cubic metre, or in the MKS system the rayl per square metre (Rayl/m²), while that of specific acoustic impedance is the pascal-second per metre (Pa·s/m), or in the MKS system the rayl (Rayl). There is a close analogy with electrical impedance, which measures the opposition that a system presents to the electric current resulting from a voltage applied to the system.

Plasma oscillations, also known as Langmuir waves, are rapid oscillations of the electron density in conducting media such as plasmas or metals in the ultraviolet region. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency depends only weakly on the wavelength of the oscillation. The quasiparticle resulting from the quantization of these oscillations is the plasmon.

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

In electromagnetics and antenna theory, the aperture of an antenna is defined as "A surface, near or on an antenna, on which it is convenient to make assumptions regarding the field values for the purpose of computing fields at external points. The aperture is often taken as that portion of a plane surface near the antenna, perpendicular to the direction of maximum radiation, through which the major part of the radiation passes."

The Rice–Ramsperger–Kassel–Marcus (RRKM) theory is a theory of chemical reactivity. It was developed by Rice and Ramsperger in 1927 and Kassel in 1928 and generalized in 1952 by Marcus who took the transition state theory developed by Eyring in 1935 into account. These methods enable the computation of simple estimates of the unimolecular reaction rates from a few characteristics of the potential energy surface.

Fluorescence cross-correlation spectroscopy (FCCS) is a spectroscopic technique that examines the interactions of fluorescent particles of different colours as they randomly diffuse through a microscopic detection volume over time, under steady conditions.

f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.

In astrophysics, particularly the study of accretion disks, the epicyclic frequency is the frequency at which a radially displaced fluid parcel will oscillate. It can be referred to as a "Rayleigh discriminant". When considering an astrophysical disc with differential rotation $, the epicyclic frequency is given by$

References

https://archive.org/stream/theoryofwavetran00consrich#page/n3/mode/2up
http://www.rexresearch.com/constran/1constran.htm
Constantinesco, G. Theory of Sonics: A Treatise on Transmission of Power by Vibrations. The Admiralty, London, 1918.
Constantinesco, G., Sonics. Trans. Soc. of Engineers, London, June 1959
Clark, R.Edison, The Man Who Made the Future. Macdonald and Jane's, London, 1977.
McNeil, I., George Constantinesco, 1881–1965 and the Development of Sonic Power Transmission. Excerpt from volume 54, Trans. of the Newcomen Society, London, 1982–83.
Constantinesco, G., A Hundred Years of Development in Mechanical Engineering. Trans. Soc. of Engineers, London, Sept. 1954.
http://www.gs-harper.com/Mining_Research/Power/Sonics005.asp
Constantinesco, G. Transmission of Power the Present, the Future. Paper read before the North East Coast Institution of Engineers and Shipbuilders in Newcastle upon Tyne, on 4 December 1925. Reprinted by order of the council. North East Coast Institution of Engineers and Shipbuilders, Newcastle upon Tyne, 1926.
https://web.archive.org/web/20090603102058/http://www.rri.ro/arh-art.shtml?lang=1&sec=9&art=3596
http://www.utcluj.ro/download/doctorat/Rezumat_Carmen_Bal.pdf
http://www.rexresearch.com/constran/1constran.htm
http://imtuoradea.ro/auo.fmte/files-2008/MECANICA_files/MARCU%20FLORIN%201.pdf
http://dynamicsflorio.webs.com/arotmm.htm

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] "Theory of wave transmission; a treatise on transmission of power by vibrations". 1922.

[2] Constantinesco, G. Theory of Sonics: A Treatise on Transmission of Power by Vibrations. The Admiralty, London, 1918

[3] "Theory of wave transmission; a treatise on transmission of power by vibrations". 1922.

[4] "Archived copy" (PDF). Archived from the original (PDF) on 4 March 2012. Retrieved 17 March 2010.{{cite web}}: CS1 maint: archived copy as title (link)

[1]

[2]

[3]

[4]