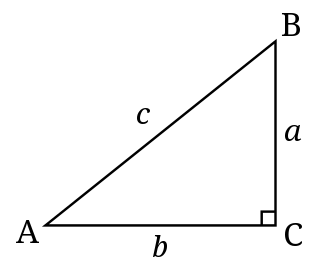
In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, for which only integer solutions are of interest. A linear Diophantine equation equates to a constant the sum of two or more monomials, each of degree one. An exponential Diophantine equation is one in which unknowns can appear in exponents.
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques.

In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (n), and the constant sum is called the 'magic constant'. If the array includes just the positive integers , the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square.
In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length and if every other problem that can be solved in polynomial space can be transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE.

The Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to one of the other rods, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- No disk may be placed on top of a disk that is smaller than it.
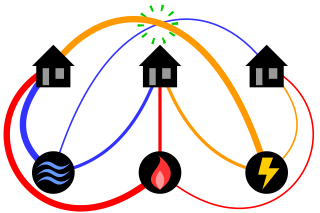
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is divisible by 2, and odd if it is not. For example, −4, 0, and 82 are even numbers, while −3, 5, 7, and 21 are odd numbers.

A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces in which the solution is to manipulate the whole object or parts of it. While puzzles of this type have been in use by humanity as early as the 3rd century BC, one of the most well-known mechanical puzzles of modern day is the Rubik's Cube, invented by the Hungarian architect Ernő Rubik in 1974. The puzzles are typically designed for a single player, where the goal is for the player to discover the principle of the object, rather than accidentally coming up with the right solution through trial and error. With this in mind, they are often used as an intelligence test or in problem solving training.

Rubik's Magic, like the Rubik's Cube, is a mechanical puzzle invented by Ernő Rubik and first manufactured by Matchbox in the mid-1980s.
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient for a function to be called one-way.

The 15 Puzzle is a sliding puzzle. It has 15 square tiles numbered 1 to 15 in a frame that is 4 tile positions high and 4 tile positions wide, with one unoccupied position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.
Verbal arithmetic, also known as alphametics, cryptarithmetic, cryptarithm or word addition, is a type of mathematical game consisting of a mathematical equation among unknown numbers, whose digits are represented by letters of the alphabet. The goal is to identify the value of each letter. The name can be extended to puzzles that use non-alphabetic symbols instead of letters.

The Megaminx or Mégaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's Cube.

The two envelopes problem, also known as the exchange paradox, is a paradox in probability theory. It is of special interest in decision theory and for the Bayesian interpretation of probability theory. It is a variant of an older problem known as the necktie paradox. The problem is typically introduced by formulating a hypothetical challenge like the following example:
Imagine you are given two identical envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?

Baguenaudier, also known as the Chinese rings, Cardan's suspension, Cardano's rings, Devil's needle or five pillars puzzle, is a disentanglement puzzle featuring a loop which must be disentangled from a sequence of rings on interlinked pillars. The loop can be either string or a rigid structure.
God's algorithm is a notion originating in discussions of ways to solve the Rubik's Cube puzzle, but which can also be applied to other combinatorial puzzles and mathematical games. It refers to any algorithm which produces a solution having the fewest possible moves. The allusion to the deity is based on the notion that an omniscient being would know an optimal step from any given configuration.
A balance puzzle or weighing puzzle is a logic puzzle about balancing items—often coins—to determine which holds a different value, by using balance scales a limited number of times. These differ from puzzles that assign weights to items, in that only the relative mass of these items is relevant.
The original Rubik's cube was a mechanical 3×3×3 cube puzzle invented in 1974 by the Hungarian sculptor and professor of architecture Ernő Rubik. Extensions of the Rubik's cube have been around for a long time and come in both hardware and software forms. The major extension have been the availability of cubes of larger size and the availability of the more complex cubes with marked centres. The properties of Rubik’s family cubes of any size together with some special attention to software cubes is the main focus of this article. Many properties are mathematical in nature and are functions of the cube size variable.
The monkey and the coconuts is a mathematical puzzle in the field of Diophantine analysis that originated in a short story involving five sailors and a monkey on a desert island who divide up a pile of coconuts; the problem is to find the number of coconuts in the original pile. The problem is notorious for its confounding difficulty to unsophisticated puzzle solvers, though with the proper mathematical approach, the solution is trivial. The problem has become a staple in recreational mathematics collections.















