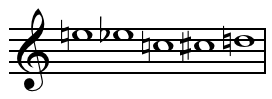In music theory a diatonic scale is a heptatonic (seven-note) scale that includes five whole steps and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps. In other words, the half steps are maximally separated from each other.
In music, a tone row or note row, also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.
In music theory, a tetrachord is a series of four notes separated by three intervals. In traditional music theory, a tetrachord always spanned the interval of a perfect fourth, a 4:3 frequency proportion —but in modern use it means any four-note segment of a scale or tone row, not necessarily related to a particular tuning system.
In music, two written notes have enharmonic equivalence if they produce the same pitch but are notated differently. Similarly, written intervals, chords, or key signatures are considered enharmonic if they represent identical pitches that are notated differently. The term derives from Latin enharmonicus, in turn from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος, from ἐν ('in') and ἁρμονία ('harmony').
Articles related to music include:

The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and twelve-note composition—is a method of musical composition. The technique is a means of ensuring that all 12 notes of the chromatic scale are sounded equally often in a piece of music while preventing the emphasis of any one note through the use of tone rows, orderings of the 12 pitch classes. All 12 notes are thus given more or less equal importance, and the music avoids being in a key.
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.
In music theory, a trichord is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In music using the twelve tone technique, combinatoriality is a quality shared by twelve-tone tone rows whereby each section of a row and a proportionate number of its transformations combine to form aggregates. Much as the pitches of an aggregate created by a tone row do not need to occur simultaneously, the pitches of a combinatorially created aggregate need not occur simultaneously. Arnold Schoenberg, creator of the twelve-tone technique, often combined P-0/I-5 to create "two aggregates, between the first hexachords of each, and the second hexachords of each, respectively."

In music theory, complement refers to either traditional interval complementation, or the aggregate complementation of twelve-tone and serialism.
In the musical system of ancient Greece, genus is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus calls some patterns of rhythm "genera".
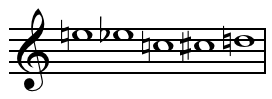
A set in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.

In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. Other names include: ic vector, PIC vector and APIC vector

Jennifer Helen McLeod was a New Zealand composer and professor of music at Victoria University of Wellington. She composed several major works for big groups including Under the Sun for four orchestras and 450 children, and the opera Hōhepa.
An all-interval tetrachord is a tetrachord, a collection of four pitch classes, containing all six interval classes. There are only two possible all-interval tetrachords, when expressed in prime form. In set theory notation, these are [0,1,4,6] (4-Z15) and [0,1,3,7] (4-Z29). Their inversions are [0,2,5,6] (4-Z15b) and [0,4,6,7] (4-Z29b). The interval vector for all all-interval tetrachords is [1,1,1,1,1,1].

Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.
The musical system of ancient Greece evolved over a period of more than 500 years from simple scales of tetrachords, or divisions of the perfect fourth, into several complex systems encompassing tetrachords and octaves, as well as octave scales divided into seven to thirteen intervals.

In music, the all-trichord hexachord is a unique hexachord that contains all twelve trichords, or from which all twelve possible trichords may be derived. The prime form of this set class is {012478} and its Forte number is 6-Z17. Its complement is 6-Z43 and they share the interval vector of <3,2,2,3,3,2>.