
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel.
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group.

A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure. For example, the cyclic group of addition modulo n can be obtained from the group of integers under addition by identifying elements that differ by a multiple of n and defining a group structure that operates on each such class as a single entity. It is part of the mathematical field known as group theory.

In mathematics, a Lie algebra is a vector space together with an operation called the Lie bracket, an alternating bilinear map , that satisfies the Jacobi identity. The vector space together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative.

In mathematics, a group is a set equipped with an operation that combines any two elements to form a third element while being associative as well as having an identity element and inverse elements. These three conditions, called group axioms, hold for number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The formulation of the axioms is, however, detached from the concrete nature of the group and its operation. This allows one to handle entities of very different mathematical origins in a flexible way, while retaining essential structural aspects of many objects in abstract algebra and beyond. The ubiquity of groups in numerous areas—both within and outside mathematics—makes them a central organizing principle of contemporary mathematics.
In mathematics, profinite groups are topological groups that are in a certain sense assembled from finite groups. They share many properties with their finite quotients: for example, both Lagrange's theorem and the Sylow theorems generalise well to profinite groups.

In group theory, a branch of mathematics, given a group G under a binary operation ∗, a subset H of G is called a subgroup of G if H also forms a group under the operation ∗. More precisely, H is a subgroup of G if the restriction of ∗ to H × H is a group operation on H. This is usually denoted H ≤ G, read as "H is a subgroup of G".
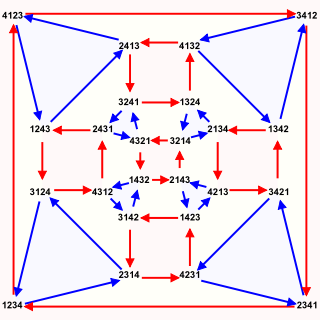
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .

An exact sequence is a sequence of morphisms between objects such that the image of one morphism equals the kernel of the next.
In mathematics, specifically group theory, the index of a subgroup H in a group G is the number of left cosets of H in G, or equivalently, the number of right cosets of H in G. The index is denoted or or . Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula
In mathematics, group cohomology is a set of mathematical tools used to study groups using cohomology theory, a technique from algebraic topology. Analogous to group representations, group cohomology looks at the group actions of a group G in an associated G-moduleM to elucidate the properties of the group. By treating the G-module as a kind of topological space with elements of representing n-simplices, topological properties of the space may be computed, such as the set of cohomology groups . The cohomology groups in turn provide insight into the structure of the group G and G-module M themselves. Group cohomology plays a role in the investigation of fixed points of a group action in a module or space and the quotient module or space with respect to a group action. Group cohomology is used in the fields of abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper. As in algebraic topology, there is a dual theory called group homology. The techniques of group cohomology can also be extended to the case that instead of a G-module, G acts on a nonabelian G-group; in effect, a generalization of a module to non-Abelian coefficients.

A group is a set together with an associative operation which admits an identity element and such that every element has an inverse.
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2 × 2 integer matrices of determinant 1, in which the off-diagonal entries are even. More generally, the notion of congruence subgroup can be defined for arithmetic subgroups of algebraic groups; that is, those for which we have a notion of 'integral structure' and can define reduction maps modulo an integer.
In mathematics, more specifically in group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no non-trivial abelian quotients. In symbols, a perfect group is one such that G(1) = G, or equivalently one such that Gab = {1}.

In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group of a group G. It was introduced by Issai Schur (1904) in his work on projective representations.
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory.
In algebra, an augmentation ideal is an ideal that can be defined in any group ring.
The Artin reciprocity law, which was established by Emil Artin in a series of papers, is a general theorem in number theory that forms a central part of global class field theory. The term "reciprocity law" refers to a long line of more concrete number theoretic statements which it generalized, from the quadratic reciprocity law and the reciprocity laws of Eisenstein and Kummer to Hilbert's product formula for the norm symbol. Artin's result provided a partial solution to Hilbert's ninth problem.
In the mathematical field of group theory, an Artin transfer is a certain homomorphism from an arbitrary finite or infinite group to the commutator quotient group of a subgroup of finite index. Originally, such mappings arose as group theoretic counterparts of class extension homomorphisms of abelian extensions of algebraic number fields by applying Artin's reciprocity maps to ideal class groups and analyzing the resulting homomorphisms between quotients of Galois groups. However, independently of number theoretic applications, a partial order on the kernels and targets of Artin transfers has recently turned out to be compatible with parent-descendant relations between finite p-groups, which can be visualized in descendant trees. Therefore, Artin transfers provide a valuable tool for the classification of finite p-groups and for searching and identifying particular groups in descendant trees by looking for patterns defined by the kernels and targets of Artin transfers. These strategies of pattern recognition are useful in purely group theoretic context, as well as for applications in algebraic number theory concerning Galois groups of higher p-class fields and Hilbert p-class field towers.
In the mathematical field of algebraic number theory, the concept of principalization refers to a situation when, given an extension of algebraic number fields, some ideal of the ring of integers of the smaller field isn't principal but its extension to the ring of integers of the larger field is. Its study has origins in the work of Ernst Kummer on ideal numbers from the 1840s, who in particular proved that for every algebraic number field there exists an extension number field such that all ideals of the ring of integers of the base field become principal when extended to the larger field. In 1897 David Hilbert conjectured that the maximal abelian unramified extension of the base field, which was later called the Hilbert class field of the given base field, is such an extension. This conjecture, now known as principal ideal theorem, was proved by Philipp Furtwängler in 1930 after it had been translated from number theory to group theory by Emil Artin in 1929, who made use of his general reciprocity law to establish the reformulation. Since this long desired proof was achieved by means of Artin transfers of non-abelian groups with derived length two, several investigators tried to exploit the theory of such groups further to obtain additional information on the principalization in intermediate fields between the base field and its Hilbert class field. The first contributions in this direction are due to Arnold Scholz and Olga Taussky in 1934, who coined the synonym capitulation for principalization. Another independent access to the principalization problem via Galois cohomology of unit groups is also due to Hilbert and goes back to the chapter on cyclic extensions of number fields of prime degree in his number report, which culminates in the famous Theorem 94.


















