Trapezoid graph

Last updated February 21, 2021

In graph theory, trapezoid graphs are intersection graphs of trapezoids between two horizontal lines. They are a class of co-comparability graphs that contain interval graphs and permutation graphs as subclasses. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect. Trapezoid graphs were introduced by Dagan, Golumbic, and Pinter in 1988. There exists ${O}(n\log n)$ algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique.

Definitions and characterizations

Given a channel, a pair of two horizontal lines, a trapezoid between these lines is defined by two points on the top and two points on the bottom line. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect. The interval order dimension of a partially ordered set, $P=(X,<)$ , is the minimum number d of interval orders P₁ … P_d such that P = P₁∩…∩P_d. The incomparability graph of a partially ordered set $P=(X,<)$ is the undirected graph $G=(X,E)$ where x is adjacent to y in G if and only if x and y are incomparable in P. An undirected graph is a trapezoid graph if and only if it is the incomparability graph of a partial order having interval order dimension at most 2.^[1]

Applications

The problems of finding maximum cliques and of coloring trapezoid graphs are connected to channel routing problems in VLSI design. Given some labeled terminals on the upper and lower side of a two-sided channel, terminals with the same label will be connected in a common net. This net can be represented by a trapezoid containing the rightmost terminals and leftmost terminals with the same label. Nets may be routed without intersection if and only if the corresponding trapezoids do not intersect. Therefore, the number of layers needed to route the nets without intersection is equal to the graph’s chromatic number.

Equivalent representations

Trapezoid representation

Trapezoids can be used to represent a trapezoid graph by using the definition of trapezoid graph. A trapezoid graph's trapezoid representation can be seen in Figure 1.

Box representation

Dominating rectangles, or box representation, maps the points on the lower of the two lines of the trapezoid representation as lying on the x-axis and that of the upper line as lying on the y-axis of the Euclidean plane. Each trapezoid then corresponds to an axis-parallel box in the plane. Using the notion of a dominance order (In R^K, x is said to be dominated by y, denoted x < y, if x_i is less than y_i for i = 1, …, k), we say that a box b dominates a box b’ if the lower corner of b dominates the upper corner of b’. Furthermore, if one of two boxes dominates the other we say that they are comparable. Otherwise, they are incomparable. Thus, two trapezoids are disjoint exactly if their corresponding boxes are comparable. The box representation is useful because the associated dominance order allows sweep line algorithms to be used.^[2]

Bitolerance graphs

Bitolerance graphs are incomparability graphs of a bitolerance order. An order is a bitolerance order if and only if there are intervals I_x and real numbers t₁(x) and t_r(x) assigned to each vertex x in such a way that x < y if and only if the overlap of I_x and I_y is less than both t_r(x) and t₁(y) and the center of I_x is less than the center of I_y.^[3] In 1993, Langley showed that the bounded bitolerance graphs are equivalent to the class of trapezoid graphs.^[4]

Relation to other families of graphs

The class of trapezoid graphs properly contains the union of interval and permutation graphs and is equivalent to the incomparability graphs of partially ordered sets having interval order dimension at most two. Permutation graphs can be seen as the special case of trapezoid graphs when every trapezoid has zero area. This occurs when both of the trapezoid’s points on the upper channel are in the same position and both points on the lower channel are in the same position.

Like all incomparability graphs, trapezoid graphs are perfect.

Circle trapezoid graphs

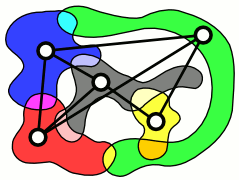
Circle trapezoid graphs are a class of graphs proposed by Felsner et al. in 1993. They are a superclass of the trapezoid graph class, and also contain circle graphs and circular-arc graphs. A circle trapezoid is the region in a circle that lies between two non-crossing chords and a circle trapezoid graph is the intersection graph of families of circle trapezoids on a common circle. There is an $O(n^{2})$ algorithm for maximum weighted independent set problem and an ${O}(n^{2}\log n)$ algorithm for the maximum weighted clique problem.

k-Trapezoid graphs

k-Trapezoid graphs are an extension of trapezoid graphs to higher dimension orders. They were first proposed by Felsner, and they rely on the definition of dominating boxes carrying over to higher dimensions in which a point x is represented by a vector $(x_{1},\ldots ,x_{k})$ . Using (k − 1)-dimensional range trees to store and query coordinates, Felsner’s algorithms for chromatic number, maximum clique, and maximum independent set can be applied to k-trapezoid graphs in ${O}(n\log ^{k-1}n)$ time.

Algorithms

Algorithms for trapezoid graphs should be compared with algorithms for general co-comparability graphs. For this larger class of graphs, the maximum independent set and the minimum clique cover problem can be solved in ${O}(n^{2}\log n)$ time.^[5] Dagan et al. first proposed an ${O}(nk)$ algorithm for coloring trapezoid graphs, where n is the number of nodes and k is the chromatic number of the graph. Later, using the box representation of trapezoid graphs, Felsner published ${O}(n\log n)$ algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique. These algorithms all require ${O}(n)$ space. These algorithms rely on the associated dominance in the box representation that allows sweeping line algorithms to be used. Felsner proposes using balanced trees that can do insert, delete, and query operations in ${O}(\log n)$ time, which results in ${O}(n\log n)$ algorithms.

Recognition

To determine if a graph ${G}$ is a trapezoid graph, search for a transitive orientation ${F}$ on the complement of ${G}$ . Since trapezoid graphs are a subset of co-comparability graphs, if ${G}$ is a trapezoid graph, its complement ${G'}$ must be a comparability graph. If a transitive orientation ${F}$ of the complement ${G'}$ does not exist, ${G}$ is not a trapezoid graph. If ${F}$ does exist, test to see if the order given by ${F}$ is a trapezoid order. The fastest algorithm for trapezoid order recognition was proposed by McConnell and Spinrad in 1994, with a running time of $O(n^{2})$ . The process reduces the interval dimension 2 question to a problem of covering an associated bipartite graph by chain graphs (graphs with no induced 2K₂).^[6] Using vertex splitting, the recognition problem for trapezoid graphs was shown by Mertzios and Corneil to succeed in $O(n(n+m))$ time, where $m$ denotes the number of edges. This process involves augmenting a given graph ${G}$ , and then transforming the augmented graph by replacing each of the original graph’s vertices by a pair of new vertices. This “split graph” is a permutation graph with special properties if an only if ${G}$ is a trapezoid graph.^[7]

Notes

↑ Ido Dagan, Martin Charles Golumbic, and Ron Yair Pinter. Trapezoid graphs and their coloring. Discrete Appl. Math., 35–46, 1988.
↑ Stefan Felsner, Rudolf Muller, and Lorenz Wernisch. Trapezoid graphs and generalizations, geometry and algorithms. In Algorithm theory—SWAT ’94 (Aarhus, 1994), volume 824 of Lecture Notes in Comput. Sci., pages 143–154. Springer, Berlin, 1994.
↑ Kenneth P. Bogart, Garth Isaak. Proper and unit bitolerance orders and graphs. Discrete Mathematics 181(1–3): 37–51 (1998).
↑ Martin Charles Golumbic and Irith B.-A. Hartman, eds., Graph Theory, Combinatorics and Algorithms: Interdisciplinary Applications, Springer-Verlag, New York, 2005
↑ R. McConnell and J. Spinrad, Linear-time modular decomposition and efficient transitive orientation of undirected graphs, Proc. 5. Ann. Symp. on Discr. Alg. (1994).
↑ Golumbic, Martin Charles, and Ann N. Trenk. Tolerance Graphs. Cambridge [u.a.: Cambridge Univ., 2004.
↑ G. B. Mertzios and D. G. Corneil. Vertex splitting and the recognition of trapezoid graphs. Discrete Applied Mathematics, 159(11), pages 1131-1147, 2011.

Related Research Articles

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

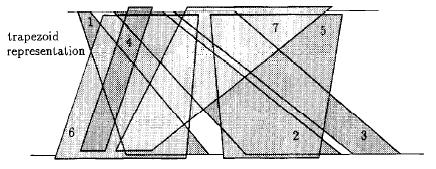
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set $of vertices such that for every two vertices in, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.$

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph $is perfect if and only if for all we have .$

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).

In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.

In graph theory, a maximal independent set (MIS) or maximal stable set is an independent set that is not a subset of any other independent set. In other words, there is no vertex outside the independent set that may join it because it is maximal with respect to the independent set property.

In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

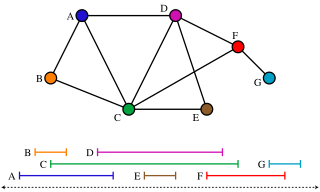
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.

In mathematics, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.

In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In graph theory, the tree-depth of a connected undirected graph G is a numerical invariant of G, the minimum height of a Trémaux tree for a supergraph of G. This invariant and its close relatives have gone under many different names in the literature, including vertex ranking number, ordered chromatic number, and minimum elimination tree height; it is also closely related to the cycle rank of directed graphs and the star height of regular languages. Intuitively, where the treewidth graph width parameter measures how far a graph is from being a tree, this parameter measures how far a graph is from being a star.

In graph theory, the graph bandwidth problem is to label the n vertices v_i of a graph G with distinct integers f(v_i) so that the quantity $is minimized . The problem may be visualized as placing the vertices of a graph at distinct integer points along the x -axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement .$

In mathematics, in the areas of order theory and combinatorics, Mirsky's theorem characterizes the height of any finite partially ordered set in terms of a partition of the order into a minimum number of antichains. It is named for Leon Mirsky (1971) and is closely related to Dilworth's theorem on the widths of partial orders, to the perfection of comparability graphs, to the Gallai–Hasse–Roy–Vitaver theorem relating longest paths and colorings in graphs, and to the Erdős–Szekeres theorem on monotonic subsequences.

In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

References

Golumbic, Martin Charles (1980). Algorithmic Graph Theory and Perfect Graphs. Academic Press. ISBN 0-444-51530-5. Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Ido Dagan, Martin Charles Golumbic, and Ron Yair Pinter. Trapezoid graphs and their coloring. Discrete Appl. Math., 35–46, 1988.

[2] Stefan Felsner, Rudolf Muller, and Lorenz Wernisch. Trapezoid graphs and generalizations, geometry and algorithms. In Algorithm theory—SWAT ’94 (Aarhus, 1994), volume 824 of Lecture Notes in Comput. Sci., pages 143–154. Springer, Berlin, 1994.

[3] Kenneth P. Bogart, Garth Isaak. Proper and unit bitolerance orders and graphs. Discrete Mathematics 181(1–3): 37–51 (1998).

[4] Martin Charles Golumbic and Irith B.-A. Hartman, eds., Graph Theory, Combinatorics and Algorithms: Interdisciplinary Applications, Springer-Verlag, New York, 2005

[5] R. McConnell and J. Spinrad, Linear-time modular decomposition and efficient transitive orientation of undirected graphs, Proc. 5. Ann. Symp. on Discr. Alg. (1994).

[6] Golumbic, Martin Charles, and Ann N. Trenk. Tolerance Graphs. Cambridge [u.a.: Cambridge Univ., 2004.

[7] G. B. Mertzios and D. G. Corneil. Vertex splitting and the recognition of trapezoid graphs. Discrete Applied Mathematics, 159(11), pages 1131-1147, 2011.

[1]

[2]

[3]

[4]

[5]

[6]

[7]