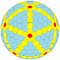
Truncated pentakis dodecahedron

Truncated pentakis dodecahedron
Conway notation	tkD
Goldberg polyhedron	GPV(3,0) or {5+,3}3,0
Fullerene	C180 [1]
Faces	92: 12 pentagons 20+60 hexagons
Edges	270 (2 types)
Vertices	180 (2 types)
Vertex configuration	(60) 5.6.6 (120) 6.6.6
Symmetry group	Icosahedral (Ih)
Dual polyhedron	Hexapentakis truncated icosahedron
Properties	convex

The truncated pentakis dodecahedron is a convex polyhedron constructed as a truncation of the pentakis dodecahedron. It is Goldberg polyhedron G_V(3,0), with pentagonal faces separated by an edge-direct distance of 3 steps.

Related polyhedra

It is in an infinite sequence of Goldberg polyhedra:

Index	GP(1,0)	GP(2,0)	GP(3,0)	GP(4,0)	GP(5,0)	GP(6,0)	GP(7,0)	GP(8,0)...
Image	D	kD	tkD
Duals	I	cD	ktI

See also

• Near-miss Johnson solid
• Truncated tetrakis cube

References

1. C180 Isomers

• Deza, A.; Deza, M.; Grishukhin, V. (1998), "Fullerenes and coordination polyhedra versus half-cube embeddings", Discrete Mathematics , 192 (1): 41–80, doi: 10.1016/S0012-365X(98)00065-X , archived from the original on 2007-02-06.
• Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF

External links

• VTML polyhedral generator Try "tkD" (Conway polyhedron notation)