Near-miss Johnson solid

In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. ^[1] The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.

Some near-misses with high symmetry are also symmetrohedra with some truly regular polygon faces.

Some near-misses are also zonohedra.

Examples

Name Conway name	Image	Vertex configurations	V	E	F	F3	F4	F5	F6	F8	F10	F12	Symmetry
Associahedron t4dP3		2 (5.5.5) 12 (4.5.5)	14	21	9		3	6					Dih3 order 12
Truncated triakis tetrahedron t6kT		4 (5.5.5) 24 (5.5.6)	28	42	16			12	4				Td, [3,3] order 24
Pentahexagonal pyritoheptacontatetrahedron		12 (3.5.3.6) 24 (3.3.5.6) 24 (3.3.3.3.5)	60	132	74	56		12	6				Th, [3+,4] order 24
Chamfered cube cC		24 (4.6.6) 8 (6.6.6)	32	48	18		6		12				Oh, [4,3] order 48
--		12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5)	30	54	26	12		12	2				D6h, [6,2] order 24
--		6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5)	27	51	26	14		12					D3h, [3,2] order 12
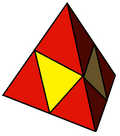
Tetrated dodecahedron		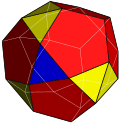4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5)	28	54	28	16		12					Td, [3,3] order 24
Chamfered dodecahedron cD		60 (5.6.6) 20 (6.6.6)	80	120	42			12	30				Ih, [5,3] order 120
Rectified truncated icosahedron atI		60 (3.5.3.6) 30 (3.6.3.6)	90	180	92	60		12	20				Ih, [5,3] order 120
Truncated truncated icosahedron ttI		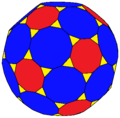120 (3.10.12) 60 (3.12.12)	180	270	92	60					12	20	Ih, [5,3] order 120
Expanded truncated icosahedron etI		60 (3.4.5.4) 120 (3.4.6.4)	180	360	182	60	90	12	20				Ih, [5,3] order 120
Snub rectified truncated icosahedron stI		60 (3.3.3.3.5) 120 (3.3.3.3.6)	180	450	272	240		12	20				I, [5,3]+ order 60

Coplanar misses

See also: Deltahedron § Non-strictly convex cases

Some failed Johnson solid candidates have coplanar faces. These polyhedra can be perturbed to become convex with faces that are arbitrarily close to regular polygons. These cases use 4.4.4.4 vertex figures of the square tiling, 3.3.3.3.3.3 vertex figure of the triangular tiling, as well as 60 degree rhombi divided double equilateral triangle faces, or a 60 degree trapezoid as three equilateral triangles. It is possible to take an infinite amount of distinct coplanar misses from sections of the cubic honeycomb (alternatively convex polycubes) or alternated cubic honeycomb, ignoring any obscured faces.

Examples: 3.3.3.3.3.3

• 
  Rhombic prism
• 
  Wedge
• 
  Trigonal trapezohedron
• 
  Gyroelongated trigonal pyramid
• 
  Triangulated monorectified tetrahedron
• 
  Elongated octahedron
• 
  Tetratetrahedron, triangulated tetrahedron
• 
  Augmented triangular cupola
• 
  Triangulated truncated triangular bipyramid
• 
  Edge-contracted icosahedron
• 
  Hexagonal prism
• 
  Hexagonal antiprism,
  Gyroelongated hexagonal pyramid
• 
  Triangular cupola
• 
  Truncated tetrahedron
• 
  Truncated octahedron

4.4.4.4

• 
  Square icositetrahedron
  (Cube)

3.4.6.4:

• 
  Hexagonal cupola
  (Degenerate)

See also

• Geodesic polyhedron
• Goldberg polyhedron
• Johnson solid
• Platonic solid
• Semiregular polyhedron
  • Archimedean solid
  • Prism
  • Antiprism

References

1. Kaplan, Craig S.; Hart, George W. (2001), "Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons", Bridges: Mathematical Connections in Art, Music and Science (PDF).

External links

• Near-miss Johnson solid, Polytope Wiki (74)
• Johnson Solid Near Misses, Polyhedra by Jim McNeil (31)
• Near Misses, Craig S. Kaplan (5)