In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, a Johnson solid is a strictly convex polyhedron, which is not uniform, and each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1); it has 1 square face and 4 triangular faces.
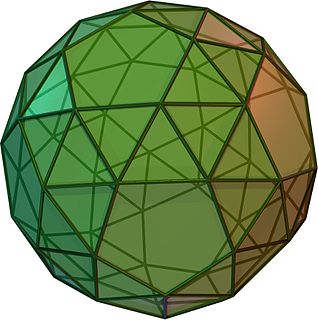
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.

In geometry, the snub disphenoid, Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron is a three-dimensional convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight deltahedra and one of the 92 Johnson solids. It can be thought of as a square antiprism where both squares are replaced with two equilateral triangles.

A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces. Hence, it is a non-regular dodecahedron.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.
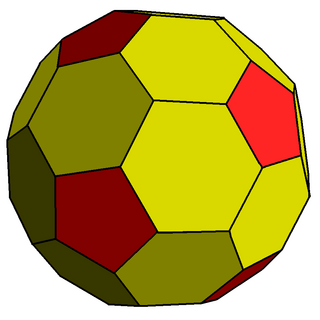
The chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (geometry) (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

The tetrated dodecahedron is a near-miss Johnson solid. It was first discovered in 2002 by Alex Doskey. It was then independently rediscovered in 2003 and named by Robert Austin.

The truncated triakis tetrahedron, or more precisely an order-6 truncated triakis tetrahedron, is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps.
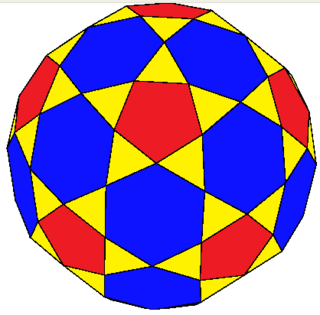
The rectified truncated icosahedron is a polyhedron, constructed as a rectified truncated icosahedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified truncated icosahedron, rectification truncating vertices down to mid-edges.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi), meaning 'twenty', and ἕδρα (hédra), meaning 'seat'. The plural can be either "icosahedra" or "icosahedrons".

In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces.



















