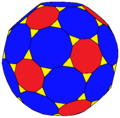
| Rectified truncated icosahedron | |
|---|---|
 | |
| Type | Near-miss Johnson solid |
| Faces | 92: 60 isosceles triangles 12 pentagons 20 hexagons |
| Edges | 180 |
| Vertices | 90 |
| Vertex configuration | 3.6.3.6  3.5.3.6  |
| Schläfli symbol | rt{3,5} |
| Conway notation | atI [1] |
| Symmetry group | Ih, [5,3], (*532) order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dual polyhedron | Rhombic enneacontahedron |
| Properties | convex |
| Net | |
 | |
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.
Contents
As a near-miss Johnson solid, under icosahedral symmetry, the pentagons are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the pentagons, having slightly different but alternating angles, causing the triangles to be isosceles instead. The shape is a symmetrohedron with notation I(1,2,*,[2])