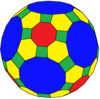
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, the gyrobifastigium is the 26th Johnson solid. It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a quarter-turn to one prism. It is the only Johnson solid that can tile three-dimensional space.
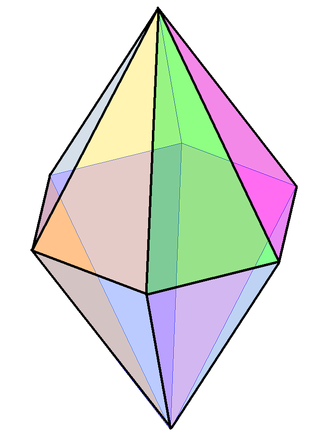
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.
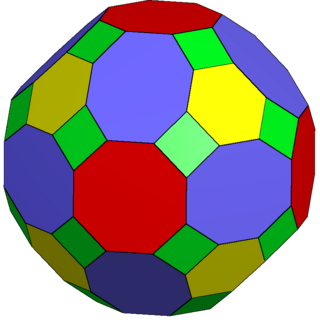
The truncated rhombicuboctahedron is a polyhedron, constructed as a truncation of the rhombicuboctahedron. It has 50 faces consisting of 18 octagons, 8 hexagons, and 24 squares. It can fill space with the truncated cube, truncated tetrahedron and triangular prism as a truncated runcic cubic honeycomb.
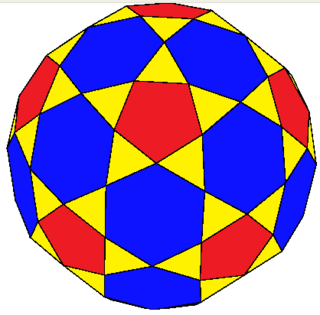
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.
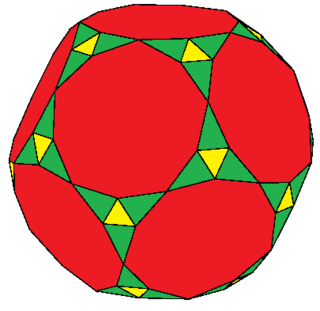
In geometry, the rectified truncated dodecahedron is a convex polyhedron, constructed as a rectified, truncated dodecahedron. It has 92 faces: 20 equilateral triangles, 60 isosceles triangles, and 12 decagons.

In geometry, the rectified truncated cube is a polyhedron, constructed as a rectified, truncated cube. It has 38 faces: 8 equilateral triangles, 24 isosceles triangles, and 6 octagons.

In geometry, the rectified truncated tetrahedron is a polyhedron, constructed as a rectified, truncated tetrahedron. It has 20 faces: 4 equilateral triangles, 12 isosceles triangles, and 4 regular hexagons.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.