In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid, with 60 isosceles triangle faces. Its dual is the truncated dodecahedron. It has also been called the kisicosahedron. It was first depicted, in a non-convex form with equilateral triangle faces, by Leonardo da Vinci in Luca Pacioli's Divina proportione, where it was named the icosahedron elevatum. The capsid of the Hepatitis A virus has the shape of a triakis icosahedron.
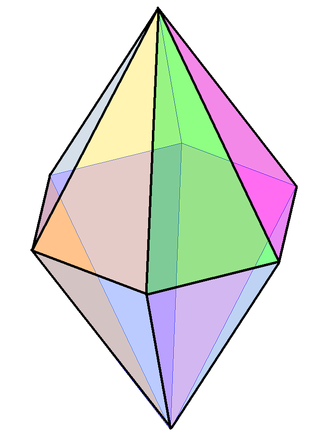
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.

In geometry, a bicupola is a solid formed by connecting two cupolae on their bases.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.
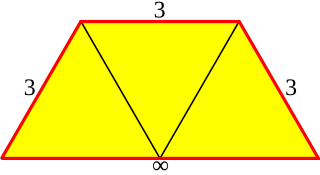
In geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.

In geometry, the pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the truncated rhombic triacontahedron.

In geometry, a tetrahedrally diminished dodecahedron is a topologically self-dual polyhedron made of 16 vertices, 30 edges, and 16 faces.
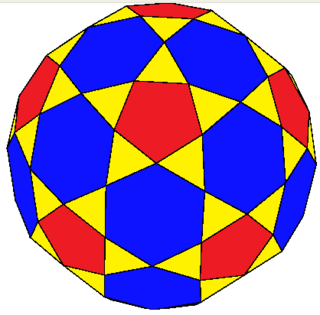
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.

In geometry, the rectified truncated octahedron is a convex polyhedron, constructed as a rectified, truncated octahedron. It has 38 faces: 24 isosceles triangles, 6 squares, and 8 hexagons.

In geometry, the rectified truncated cube is a polyhedron, constructed as a rectified, truncated cube. It has 38 faces: 8 equilateral triangles, 24 isosceles triangles, and 6 octagons.

In geometry, the rectified truncated tetrahedron is a polyhedron, constructed as a rectified, truncated tetrahedron. It has 20 faces: 4 equilateral triangles, 12 isosceles triangles, and 4 regular hexagons.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".

In geometry, a rectified prism is one of an infinite set of polyhedra, constructed as a rectification of an n-gonal prism, truncating the vertices down to the midpoint of the original edges. In Conway polyhedron notation, it is represented as aPn, an ambo-prism. The lateral squares or rectangular faces of the prism become squares or rhombic faces, and new isosceles triangle faces are truncations of the original vertices.























